TSP的几个算法
这是一个自己做的ppt的记录。
TSP实例
有一位商人,他想访问德国的某些城市,要求:
- 所走路程最短;
- 每个城市只能访问一次;
- 从某城市出发,最后回到该城市。
让我们看一下为什么要学这个问题,主要来看一下tsp到底有什么用。
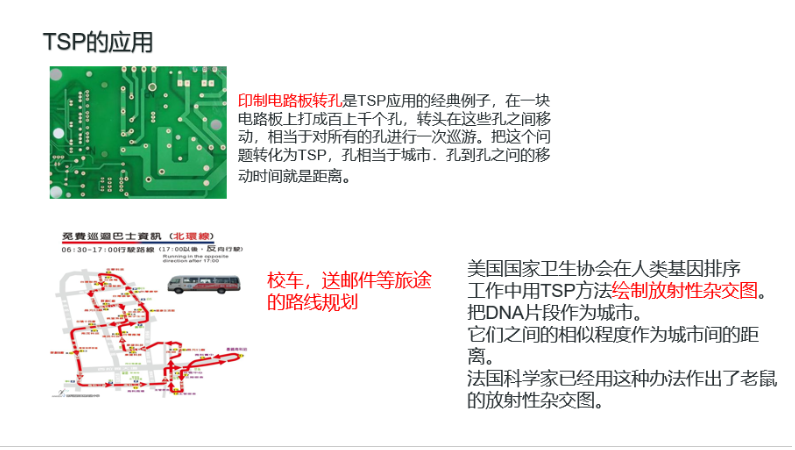
看完了应用,我们来看一下怎么去解决这个问题吧
首先先任意选一个点作为起点,然后开始连接就可以看到有n!种情况
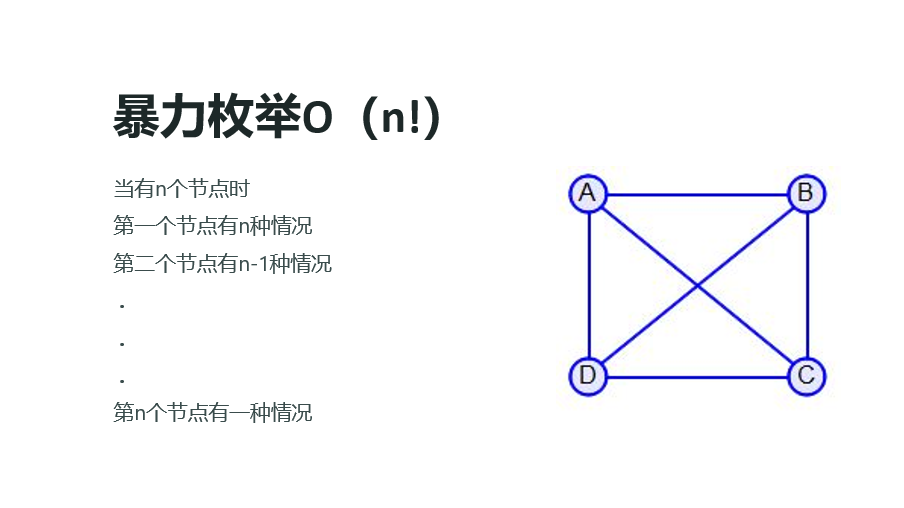
动态规划
我们尝试优化一下,目前最好的优化是通过动态规划去解决,复杂度为o(2^n*n^2)
首先得懂得为什么可以使用动态规划,动态规划就是在求解一个复杂问题时,将其分解为若干个简单问题。通过求解简单问题的最优解,来找到目标问题的最优解。
使用动态规划,需要问题本身有最优子结构,我们需要找到要解决的问题的子问题。
现在找一下tsp的最优子结构
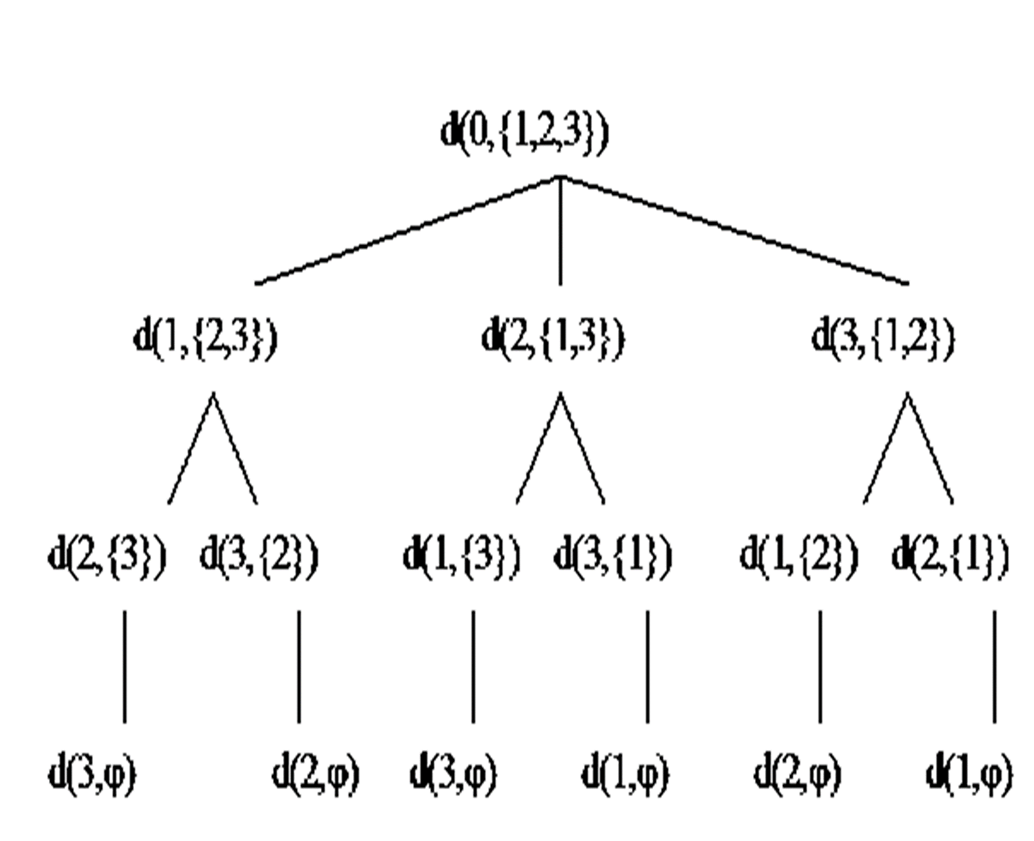
1 | 从0出发,经过[1,2,3]这几个城市,然后回到0,使得花费最少。要实现这个要求,需要从下面三个实现方案中选择花费最少的方案。 |
1、 从0出发,到1,然后再从1出发,经过[2,3]这几个城市,然后回到0,使得花费最少。
2、 从0出发,到2,然后再从2出发,经过[1,3]这几个城市,然后回到0,使得花费最少。
3、 从0出发,到3,然后再从3出发,经过[1,2]这几个城市,然后回到0,使得花费最少。
可以发现,三个小的解决方案的最优解,构成了大的解决方案,所以这个问题具有最优子结构,可以用动态规划来实现。

注意
这个算法由于空间复杂度有o(n*2^n),所以做一般的算法题要用到状态压缩,用0代表没有到达该城市,1代表去过该城市。例如:11011代表1-5个城市只有第三个城市没去过。上述的S集合就是通过状压保存。
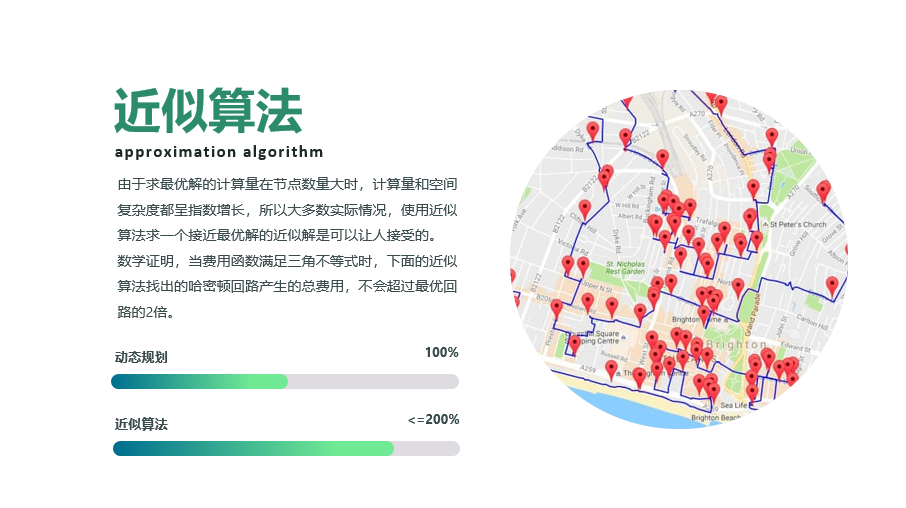
说了这么多,看一下怎么解决,主要分为4个步骤。
步骤
(1)选择G的任意一个顶点r作为根节点(出发/结束点)
(2)用Prim算法找出G的一棵以r为根的最小生成树T
(3)前序遍历访问树T,得到遍历顺序组成的顶点表L
(4)将r加到顶点表L的末尾,按L中顶点的次序组成哈密顿回路H
简单的解释一下其中的名词,有需要自己了解
prim算法
Prim算法如何进行计算?
①选定一个起点做为一个集合 a ,剩下的点为另一个集合 b
②将横跨两个集合且权重在其中最小的边加入最小生成树
③将刚刚加入最小生成树的边中不在集合 a 中的点加入集合 a,直到所有的点加入集合 a
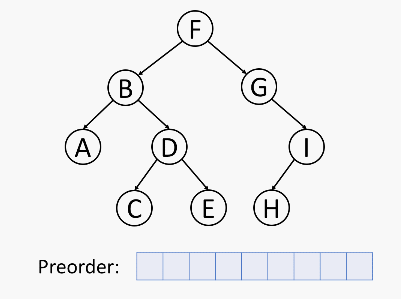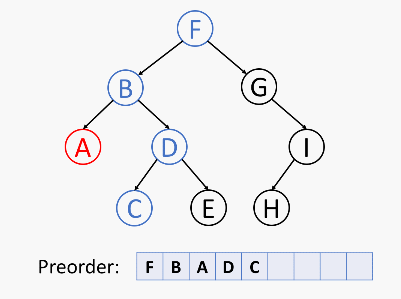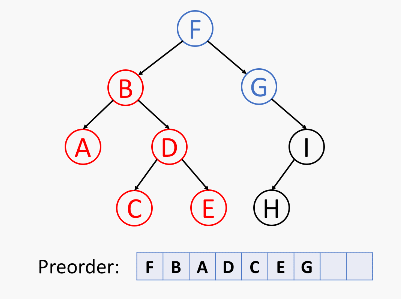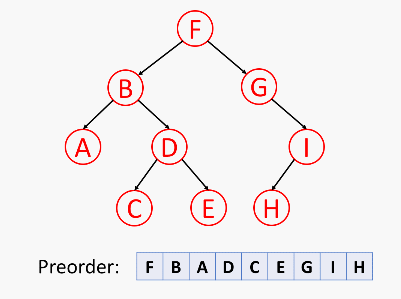
前序遍历
首先访问根节点,然后遍历左子树,最后遍历右子树。
遗传算法
定义
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
步骤

这里补充一下细节:
- 交叉操作:随机挑取在染色体(路径)上的一个序号(2-n-1)交换两条染色体序号后面的(基因),这里需要进行基因冲突处理,即交换后要检查是否交换过来了已有的基因,如果是则和另一条的重复基因交换。
- 变异操作,对一条基因选出i,j(0<i<j<=n)将其中的基因交换。
本文链接:
https://ioaol.github.io/TSPppt.html