leetcode笔记
2021-04-21 / IOAOl   

以下题目均为leetcode的题目，仅作为个人笔记，侵权联删。

栈

Easy

删除最外层的括号

有效括号字符串为空 (“”)、”(“ + A + “)” 或 A + B，其中 A 和 B 都是有效的括号字符串，+ 代表字符串的连接。例如，””，”()”，”(())()” 和 “(()(()))” 都是有效的括号字符串。

如果有效字符串 S 非空，且不存在将其拆分为 S = A+B 的方法，我们称其为原语（primitive），其中 A 和 B 都是非空有效括号字符串。

给出一个非空有效字符串 S，考虑将其进行原语化分解，使得：S = P_1 + P_2 + … + P_k，其中 P_i 是有效括号字符串原语。

对 S 进行原语化分解，删除分解中每个原语字符串的最外层括号，返回 S 。

思路：栈判断是否组成完整的原语，直接substr消除最外层的符号。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    string removeOuterParentheses(string S) {
        int stackint=0;
        int left=0;
        string res;
        for(int i=0;i<S.size();i++){
            if(S[i]=='('){
                stackint++;
            }else{
                stackint--;
            }
            if(stackint==0){
               res=res+S.substr(left+1,i-left-1);
               left=i+1;
            }
        }
        return res;
    }
};

最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。

思路：设计一个辅助栈，给每个元素都配上一个当前最小值，跟随原来栈来增减.

$\textcolor{red}{注意点:辅助栈要先放入一个最大值，在第一个元素放入的时候方便更新。}$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class MinStack {

    /** initialize your data structure here. */
    Deque<Integer> MainStack;
    Deque<Integer> assistStack;
    public MinStack() {
        MainStack=new LinkedList<Integer>();
        assistStack=new LinkedList<Integer>();
        assistStack.push(Integer.MAX_VALUE);
    }
  
    public void push(int x) {
        MainStack.push(x);
        if(x<assistStack.peek())
            assistStack.push(x);
        else{
            assistStack.push(assistStack.peek());
        }
    }
  
    public void pop() {
        MainStack.pop();
        assistStack.pop();
    }
  
    public int top() {
        return MainStack.peek();
    }
  
    public int getMin() {
        return assistStack.peek();
    }
}

比较含退格的字符串

给定 S 和 T 两个字符串，当它们分别被输入到空白的文本编辑器后，判断二者是否相等，并返回结果。 # 代表退格字符。

注意：如果对空文本输入退格字符，文本继续为空。

示例 1：

输入：S = “ab#c”, T = “ad#c”
输出：true
解释：S 和 T 都会变成 “ac”。

思路：模拟，遇到‘#’就判断栈是否为空，不空则弹出，遇到其他符号就入栈。

时间复杂度O(n+m)

空间复杂度O(n+m)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    bool backspaceCompare(string s, string t) {
        stack<char> s1;
        stack<char> s2;
        for(int i=0;i<s.size();i++){
            if(s[i]=='#'){
                if(!s1.empty())
                    s1.pop();
            }
            else s1.push(s[i]);
        }
        for(int k=0;k<t.size();k++){
            if(t[k]=='#'){
                if(!s2.empty())
                    s2.pop();
            }
            else s2.push(t[k]);
        }
        return s1==s2;
    }
};

思路2：从后往前遍历，每次都先jump到有效位置，进行比较。

注意：①跳过的时候要看跳的时候是否有‘#’。

②要两个字符串分析完才能结束。

时间复杂度O(n+m)

空间复杂度O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int jump(string & str ,int i){
        int count=0;
        while(i>=0){
            if(str[i]=='#')
                count++;
            else if(count)
                --count;
            else break;
            i--;
        }
        return i;
    }
    bool backspaceCompare(string s, string t) {
        int i=s.size()-1;
        int j=t.size()-1;
        while(i>=0||j>=0){
            i=jump(s,i);
            j=jump(t,j);
            if(i<0||j<0) break;
            if(s[i--]!=t[j--])return false;
        }
        return i<0&&j<0;
    }
};

整理字符串

一个整理好的字符串中，两个相邻字符 s[i] 和 s[i+1]，其中 0<= i <= s.length-2 ，要满足如下条件:

若 s[i] 是小写字符，则 s[i+1] 不可以是相同的大写字符。
若 s[i] 是大写字符，则 s[i+1] 不可以是相同的小写字符。

思路用栈保存要保留的字符，遇到相同的（不同大小写的）就弹出，否则加入。

时间复杂度O(n)

空间复杂度O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    string makeGood(string s) {
        if(s.size()<2)
            return s;
        stack<char> st;
        for(int i=s.size()-1;i>=0;i--){
            if(st.empty())
                st.push(s[i]);
            else if(s[i]-'a'==st.top()-'A'||s[i]-'A'==st.top()-'a')
                st.pop();
            else
                st.push(s[i]);
        }
        string ans;
        while(!st.empty()){
            ans+=st.top();
            st.pop();
        }
        return ans;
    }
};

优化后的 string当st用

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    string makeGood(string s) {
        string ans;
        for(int i=0;i<s.size();i++){
            if(!ans.empty()&&((char)(ans.back()) ^ s[i]) == 32)
                ans.pop_back();
            else
                ans.push_back(s[i]);
        }
        return ans;
    }
};

二叉树的后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        if(root==nullptr)
            return {};
        vector<int> ans;
        stack<TreeNode*> st;
        TreeNode* prev=nullptr;
        while(root!=nullptr||!st.empty()){	//栈中还有节点或者根节点不为空可以继续遍历
            while(root){
                st.emplace(root);	//先存所有左孩子
                root=root->left;
            }
            root=st.top();	//取出最后的左孩子或者是root本身
            st.pop();
            if(root->right==nullptr||root->right==prev){	//右孩子为空或者右树已经访问完毕
                ans.emplace_back(root->val);//访问根节点
                prev=root;
                root=nullptr;	//取下一个栈中的节点
            }else{
                st.emplace(root);	//存放根节点
                root=root->right;	//访问右树
            }
        }
        return ans;
    }
};

二叉树的中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> ans;
        while(root!=nullptr||!st.empty()){		//栈中还有节点或者根节点不为空可以继续遍历
            while(root){
                st.emplace(root);		//先存所有左孩子
                root=root->left;
            }
            root=st.top();	//取出最后的左孩子或者是root本身
            st.pop();
            ans.emplace_back(root->val);	//访问根节点
            root=root->right;    //访问右树
        }
        return ans;
    }
};

二叉树的前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> ans;
        while(root!=nullptr||!st.empty()){
            while(root){
                ans.emplace_back(root->val);
                st.emplace(root);
                root=root->left;
            }
            root=st.top();
            st.pop();
            root=root->right;
        }
        return ans;
    }
};

medium

反转每对括号间的子串

给出一个字符串 s（仅含有小写英文字母和括号）。

请你按照从括号内到外的顺序，逐层反转每对匹配括号中的字符串，并返回最终的结果。

注意，您的结果中 不应 包含任何括号。

示例 3：

1
2
输入：s = "(ed(et(oc))el)"
输出："leetcode"

示例 4：

1
2
输入：s = "a(bcdefghijkl(mno)p)q"
输出："apmnolkjihgfedcbq"

思路1：栈，遇到左括号进栈，右括号出栈的同时将左右括号之间的所有元素反转。

最后将左右括号去除。

时间复杂度O($n^2$)

空间复杂度O($n$)，栈空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    string reverseParentheses(string s) {
        stack<int> st;
        for(int i=0;i<s.size();++i){
            if(s[i]=='(')
                st.push(i);//序号进栈
            else if(s[i]==')'){
                int head=st.top();
                st.pop();
                //反转中间元素
                reverse(s.begin()+head+1,s.begin()+i);
            }
        }
        string ans="";
        for(char ch:s)	//去掉括号
            if(ch!='('&&ch!=')')
                ans+=ch;
        return ans;
    }
};

思路2：先用栈遍历来记录每个括号对应的括号位置。然后遍历时每次遇到括号就跳转到对应括号，反方向遍历。每个括号会遍历两遍，每个元素会遍历一遍。

时间复杂度O($n$)

空间复杂度O($n$)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    string reverseParentheses(string s) {
        stack<int> st;
        int len=s.size();
        vector<int> pairs(len);		//记录每个括号对应的括号位置
        for(int i=0;i<len;++i){
            if(s[i]=='(')
                st.push(i);
            else if(s[i]==')'){
                int head=st.top();
                st.pop();
                pairs[i]=head;
                pairs[head]=i;
            }
        }
        int i=0;
        int dir=1;
        string ans="";
        while(i<len){
            if(s[i]=='('||s[i]==')'){
                i=pairs[i];	//跳转到对应括号
                dir=-dir;	//方向反转
            }else{
                ans+=s[i];	//保存元素
            }
            i+=dir;	//跟着dir方向走
        }
        return ans;      
    }
};

滑动窗口

easy

和为s的连续正数序列

<span id="he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof">

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。

序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

1
2
3
示例 1：
输入：target = 9
输出：[[2,3,4],[4,5]]

思路:滑动窗口，三种情况。

① 当当前窗口比target小时，窗口右端点右移。

② 当当前窗口比target大时，窗口左端点右移。

③ 当当前窗口等于target时，窗口左端点右移。

其中要一直保持左端点小于右端点。

注意：右端点上界为target/2+1,超过之后两个数相加就肯定大于target。

时间复杂度O(target)

空间复杂度O(1)

求和公式版：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<vector<int>> findContinuousSequence(int target) {
        vector<vector<int>> ans;
        int l=1,r=2;
        while(r>l){
            int sum=(l+r)*(r-l+1)/2;
            if(sum==target){
                vector<int> newlist;
                for(int j=l;j<=r;j++)
                    newlist.emplace_back(j);
                ans.emplace_back(newlist);
                ++l;
            }else if(sum<target)++r;
            else ++l;
        }
        return ans;
    }
};

移动窗口调整sum版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<vector<int>> findContinuousSequence(int target) {
        vector<vector<int>> ans;
        int l=1,r=2,sum=3;
        while(r>l){
            if(sum==target){
                vector<int> newlist;
                for(int j=l;j<=r;++j)
                    newlist.emplace_back(j);
                ans.emplace_back(newlist);
            }
            if(sum<target){	//注意加的顺序
                ++r;
                sum+=r;
            }else{			//注意减的顺序
                sum-=l;
                ++l;
            }
        }
        return ans;
    }
};

medium

无重复字符的最长子串

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

1
2
3
输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

思路：滑动窗口，set存放窗口内的字母。 将i , j分别作为窗口的左右边界，没有遇到重复的就 j 右移，直到遇到\n或者在窗口内存放的字母。i右移直到遇到刚才j遇到重复字母。如此循环，在过程中记录窗口大小。

时间复杂度O(N)

空间复杂度O(|$\sum{Z}$|)字符集大小

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int l=0,r=0,ans=0,len=0;
        unordered_set<char> st;	//窗口里的字母
        while(r<s.size()){
            //窗口找不到当前右边界字母并且右边界没到字符串末尾
            while(r<s.size()&&st.find(s[r])==st.end())
                st.insert(s[r++]);	//加入窗口并更新边界
            ans=max(ans,r-l);	//更新窗口最大值
            while(r>=l){
                st.erase(s[l]);
                if(s[l++]==s[r])break;	//刚才删掉了与有边界遇到的相同字符可以退出了
            }
        }
        return ans;
    }
};

hard

最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。

注意：如果 s 中存在这样的子串，我们保证它是唯一的答案。

1
2
输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

思路：当没有覆盖t全部字母时，right右移，覆盖完了，left左移，记录区间长度最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    bool check(map<char,int>& Scount,map<char,int>& Tcount){
        auto it=Scount.begin();
        while(it!=Scount.end()){
            if((it->second)>(Tcount[it->first]))
                return false;
            it++;
        }
        return true;
    }
    string minWindow(string s, string t) {
        map<char,int> Scount;
        map<char,int> Tcount;
        for(int i=0;i<t.size();i++){
            if(Scount.find(t[i])==Scount.end()){
                Scount[t[i]]=0;
                Tcount[t[i]]=0;
            }
            Scount[t[i]]++;
        }
        int left=0,right=0;
        int ans=s.size()+22;
        int index=0;
        while(!(right>=s.size()&&!check(Scount,Tcount))){
            if(!check(Scount,Tcount)){
                if(Scount.find(s[right])!=Scount.end()){
                   Tcount[s[right]]++;
                }
                right++;
            }else{
                if(right-left<ans){
                    index=left;
                    ans=right-left;
                }
                if(Scount.find(s[left])!=Scount.end()){
                    Tcount[s[left]]--;
                }
                left++;
            }
        }
        if(ans==s.size()+22)
            return "";
        else{
            return s.substr(index,ans);
        }
    }
};

动态规划

easy

连续子数组的最大和

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

要求时间复杂度为O(n)。

示例1:

1
2
3
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

思路：动态规划，dp[i]等于nums[i]为末尾的子数组的和的最大值。寻找dp数组最大值，就为所求的解。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int ans=nums[0],pre=0,cur=nums[0];	//pre=dp[-1] ,cur=dp[0]
        for(int& num : nums){
            cur = max(num, pre + num);//当前的子数组取自己为单个的数组，还是加前面的数组
            ans = max(cur, ans);	  //更新ans
            pre = cur;				  //更新pre
        }
        return ans;
    }
}

medium

解码方法

一条包含字母 A-Z 的消息通过以下映射进行了 编码 ：

1
2
3
4
'A' -> 1
'B' -> 2
...
'Z' -> 26

要 解码 已编码的消息，所有数字必须基于上述映射的方法，反向映射回字母（可能有多种方法）。例如，"11106" 可以映射为：

  • "AAJF" ，将消息分组为 (1 1 10 6)
  • "KJF" ，将消息分组为 (11 10 6)

注意，消息不能分组为 (1 11 06) ，因为 "06" 不能映射为 "F" ，这是由于 "6" 和 "06" 在映射中并不等价。

给你一个只含数字的 非空 字符串 s ，请计算并返回 解码 方法的 总数 。

题目数据保证答案肯定是一个 32 位 的整数。

思路：动态规划，dp[i]表示0-(i-1)为之间的解码可能总数。第i个字符它可以跟i-1个字符合并为一个数也可以自己作为一个数。

注意：以上两种情况可以同时满足。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int numDecodings(string s) {
        vector<int> dp(s.size()+1,0);
        dp[0]=1;	//空串
        if(s.size()>=1)
            dp[1]=(s[0]=='0'?0:1);
        for(int i=2;i<=s.size();i++){
            int tmp=stoi(s.substr(i-2,2));
            if(tmp>=10&&tmp<=26)	//说明是两位数
                dp[i]+=dp[i-2];
            if(s[i-1]!='0')			//除了自己是0以外，都可以自己作为一个数解码
                dp[i]+=dp[i-1];
        }
        return dp[s.size()];
    }
};

股票的最大利润

买卖股票的最佳时机

与上面一道题相同。

假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

示例 1:

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

思路：当天的最大利润=今天的价格-历史最低价。dp[i]表示前i天最多能获得的利润。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()<2)
            return 0;
        int dpnum=0;    //前0天能获得的利润
        int historyMinCost=prices[0];  //历史最低价
        for(int i=1;i<prices.size();i++){
            //前i-1天最大利润和今天能获得的最大利润比较
            int curMax=max(dpnum,prices[i]-historyMinCost);
            //更新历史最低利润 
            historyMinCost=min(historyMinCost,prices[i]);
            //更新前i-1天的记录
            dpnum=curMax;
        }
        return dpnum;
    }
};

完全平方数

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

思路:dp[i]表示和为 i 的完全平方数的 最少数量

那么dp[i]可以由dp[i-jj]和j ``j得到。(1<=j<i)

找到最小组成的数量，就是所得。

时间复杂度O($nlogn$)

空间复杂度O($n$)

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1,n);
        dp[0]=0;
        for(int i=1;i<=n;++i){
            for(int j=0;j*j<=i;++j){
                dp[i]=min(dp[i],dp[i-j*j]+1);
            }
        }
        return dp[n];
    }
};

最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

1
2
3
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

思路1：dp[i]为取nums[i]为最后一个的子序列的长度。首先所有的dp[i]初始化为1

dp[i]等于dp[0]到dp[i-1]满足条件的dp[k]的最大长度+1，也就是接nums[i]前面的一段子序列的长度。接的条件是前面的元素小于num[i]。

$dp[i]=max(\sum_{k=i-1}^0dp[k])+1 $

时间复杂度O($N^2$)

空间复杂度O($N$)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> dp(nums.size(),1);//全部初始化为1，因为最少包含自己
        int ans=1;
        for(int i=1;i<nums.size();++i){
            for(int j=i-1;j>=0;--j){		//找以前的子序列
                if(nums[j]<nums[i]){		//满足接上的条件
                    dp[i]=max(dp[i],dp[j]+1);	//找接上最长的
                }
            }
            ans=max(dp[i],ans);
        }
        return ans;
    }
};

思路2：维护一个序列，尽可能的让它上升速度慢。该序列的长度就是所求

初始化：放入nums[0];

当遇到nums[i]时

  • 当nums[i]大于序列中所有元素，也就是大于序列中最后一个元素，nums[i]加入序列尾
  • 当nums[i]小于序列最大元素，也就是小于序列中最后一个元素，nums[i]替换掉第一个大于nums[i]的元素。

当查找第一个大于nums[i]的元素的时候可以使用二分查找，因为维护的序列是升序的。

时间复杂度O($NlogN$)

空间复杂度O($N$)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> tail;
        tail.emplace_back(nums[0]);//放入nums[0]
        for(int i=1;i<nums.size();++i){
            if(tail.back()<nums[i]){//当nums[i]大于序列中所有元素
                tail.emplace_back(nums[i]);
            }else{
                int left=0,right=tail.size()-1;
                while(left<=right){		//使用二分查找
                    int mid=left+(right-left)/2;
                    if(tail[mid]<nums[i]){
                        left=mid+1;
                    }else{
                        right=mid-1;
                    }
                }
                tail[left]=nums[i];//替换掉第一个大于nums[i]的元素。
            }
        }
        return tail.size();
    }
};

最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

思路：动态规划，dp [i] [j]表示i到j下标的字符串是不是回文串。

dp [i] [j]= dp [i+1] [j-1]&&s [i]==s [j]

由长度1开始遍历，注意，两个相同的字符串或者形同aba（len==3）的字符串都是是回文串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    string longestPalindrome(string s) {
        int len=s.size();
        vector<vector<bool>>dp(len,vector<bool>(len));
        for(int i=0;i<len;++i) dp[i][i]=true;
        int start=0,maxlen=1; 
        for(int L=2;L<=len;++L){	//长度
            for(int l=0;l<len;++l){	//左边界
                int r=l+L-1;		//由长度和左边界确定右边界
                if(r>=len) break;	//右边界出界
                if(s[l]==s[r]){		//两边相同
                    if(r-l<3)		//字符串长度小于等于3
                        dp[l][r]=true;
                    else			//两边相同，看里面是不是回文串
                        dp[l][r]=dp[l+1][r-1];
                }else{				//两边不相同
                    dp[l][r]=false;
                }
                if(dp[l][r]&&maxlen<L){	//记录答案
                    maxlen=L;
                    start=l;
                }
            }
        }
        return s.substr(start,maxlen);
    }
};

最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

  • 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

思路：dp [i] [j]代表字符串1用了前i个，字符串2用了前j个的最长公共子序列长度。

求dp [i] [j]

i或者j为0时没有公共子序列。dp [i] [j]=0

当字符串1的第i个和字符串2的第j个字符相同，可以由dp [i-1] [j-1]加1得到最长结果。

不同的时候，找dp [i-1] [j]和dp [i] [j-1]的最大值，因为没有可以扩展

时间复杂度O($NM$)

空间复杂度O($NM$)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m=text1.size(),n=text2.size();
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        for(int i=1;i<=m;++i){
            char c1=text1[i-1];
            for(int j=1;j<=n;++j){
                char c2=text2[j-1];
                if(c1==c2){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[m][n];
    }
};

空间优化到max（m,n）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
         if (text1.size() < text2.size()) {
            swap(text1, text2);
        }
        int m=text1.size();
        int n=text2.size();
        vector<int> dp(n+1,0);
        for(int i=1;i<=m;++i){
            int pre=dp[0];
            for(int j=1;j<=n;++j){
                if(text1[i-1]==text2[j-1]){
                    int tmp=dp[j];
                    dp[j]=pre+1;
                    pre=tmp;
                }else{
                    pre=dp[j];
                    dp[j]=max(dp[j],dp[j-1]);
                }
            }
        }
        return dp[n];
    }
};

hard

最大子矩阵

给定一个正整数、负整数和 0 组成的 N × M 矩阵，编写代码找出元素总和最大的子矩阵。

返回一个数组 [r1, c1, r2, c2]，其中 r1, c1 分别代表子矩阵左上角的行号和列号，r2, c2 分别代表右下角的行号和列号。若有多个满足条件的子矩阵，返回任意一个均可。

注意：本题相对书上原题稍作改动

示例：

1
2
3
4
5
6
7
输入：
[
   [-1,0],
   [0,-1]
]
输出：[0,1,0,1]
解释：输入中标粗的元素即为输出所表示的矩阵

说明：

  • 1 <= matrix.length, matrix[0].length <= 200

思路：压缩二维数组的列使其为一维数组，然后动态规划求一维数组的最大字序和，就可以求出该二维数组固定高（这里的高就是二维数组的高度）的子矩阵的最大值。

然后套两层循环来遍历所有的高，i为上高，j为下底，有了i和j就可以唯一确定矩阵的高。

时间复杂度O（$nm^2$）

空间复杂度O（$n$）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<int> getMaxMatrix(vector<vector<int>>& matrix) {
        int r1,c1,r2,c2,maxval=INT_MIN;			//初始化矩阵最大值
        int m=matrix.size(),n=matrix[0].size();
        int tmp1,tmp2;		//用于保存求一维数组最大字段和的起点。
        vector<int> colsum(n,0);		//压缩后的一维矩阵
        for(int i=0;i<m;++i){			//遍历上高
            fill(colsum.begin(),colsum.end(),0);	//上高变化时，将一维数组初始化
            for(int j=i;j<m;++j){		//遍历下底
                int sum=0;			//开始求最大字序和
                for(int k=0;k<n;++k){
                    colsum[k]+=matrix[j][k];
                    if(sum>0){		//前面的+现在的 可以变得更大
                        sum+=colsum[k];
                    }else{			//抛弃前面的，从现在开始重新计算
                        sum=colsum[k];
                        tmp1=i;		//记录上高
                        tmp2=k;		//记录左边界
                    }
                    if(maxval<sum){		//更新答案
                        maxval=sum;
                        r1=tmp1;		//拿到之前记录的上高
                        c1=tmp2;		//拿到之前记录的左边界
                        r2=j;			//记录当前的下底
                        c2=k;			//记录当前的右边界
                    }
                }
            }
        }
        return {r1,c1,r2,c2};
    }
};

奇怪的打印机

有台奇怪的打印机有以下两个特殊要求：

  • 打印机每次只能打印由 同一个字符 组成的序列。
  • 每次可以在任意起始和结束位置打印新字符，并且会覆盖掉原来已有的字符。

给你一个字符串 s ，你的任务是计算这个打印机打印它需要的最少打印次数。

示例 1：

1
2
3
输入：s = "aaabbb"
输出：2
解释：首先打印 "aaa" 然后打印 "bbb"。

思路：动态规划，dp[i][j]代表i到j至少需要打印的次数。

首先压缩字符串。aaabbb等价于ab，连续相同的字符串可以看做一个字符

推导 dp[i][j]，

当 i==j时显然等于1

当 s[i]==s[j]时在打印 i时可以打印 j，所以 dp[i][j]=dp[i][j-1]

当 s[i]!=s[j]时，可以将 i-j分割为 i-k和 k-j(i<=k<j)

后往前推版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int strangePrinter(string s) {
        string str;
        char pre=s[0];
        str.push_back(pre);
        for(int i=1;i<s.size();++i){
            if(s[i]==pre)
                continue;
            pre=s[i];
            str.push_back(s[i]);
        }
        swap(s,str);	//压缩s
        int n = s.length();
        vector<vector<int>> dp(n, vector<int>(n));
        for (int i = n - 1; i >= 0; i--) {	//从后往前推导
            dp[i][i] = 1;//长度1的都为1
            for (int j = i + 1; j < n; j++) { 	//j往后拓展
                if (s[i] == s[j]) {
                    dp[i][j] = dp[i][j - 1];	//j-1在前一步推导过了
                } else {
                    int minn = INT_MAX;
                    for (int k = i; k < j; k++) {
                        //k+1>i并且i<k<j所以都是推导过的
                        //分割成i-k和k+1-j的，找最小次数
                        minn = min(minn, dp[i][k] + dp[k + 1][j]);
                    }
                    dp[i][j] = minn;
                }
            }
        }
        return dp[0][n - 1];
    }
};

向后推版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<vector<int>> dp(n,vector<int>(n,INT_MAX/4));
       for(int j=0;j<n;++j){	//右边界j往后推,右边界小于j的都被推导过
           dp[j][j]=1;			//长度1的都为1
           for(int i=j-1;i>=0;--i){	//i在j的基础上往前推，左边界小于j，大于i的都被推导过
               if(s[i]==s[j])	//在给j打印的时候打印i
                   dp[i][j]=dp[i+1][j];	//dp[i+1][j]是前一步推导
               else{
                   for(int k=j;k>i;k--)
                   	//i<k<=j，所以k-1<=j-1,dp[i][k-1]已经推导过
                   	//同理，i<k, dp[k][j]也推导过
                       dp[i][j]=min(dp[i][j],dp[i][k-1]+dp[k][j]);
               }
           }
       }

根据长度推导

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector<vector<int>> dp(n,vector<int>(n,INT_MAX/4));
for(int i=0;i<n;i++)	//长度1的都为1
          dp[i][i]=1;
      for(int len=2;len<=n;++len){			//区间长度
          for(int i=0,j=len-1;j<n;j++,i++){	//保持[i,j]长度为len
              if(s[i]==s[j]) 
                  //i可以和i+1-j的左边界一起打印或者
                  //j可以和i-j-1的右边界一起打印
                  dp[i][j]=min(dp[i+1][j],dp[i][j-1]);
              else{
                  dp[i][j]=INT_MAX;
                  //i-k和k+1-j的长度肯定小于i-j,所以一定被推导过
                  for(int k=i;k<j;++k)
                      dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
              }
          }
      }
      return dp[0][n - 1];

递归版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int strangePrinter(string s) {
        int n = str.size();
        //dp[i][j]表示从第i个字符到第j个字符（包括两端）需要的打印次数
        vector<vector<int>> dp(n+1, vector<int>(n+1, -1));
        return helper(1,n,dp,str);
    }
    int helper(int l, int r, vector<vector<int>>& dp, string& str) {
        if (dp[l][r] != -1) return dp[l][r];//说明已经求得直接返回
        if (l > r) return dp[l][r] = 0;		//无效区间
        //求区间l到r-1,最后打印r, r自己打印
        int res = helper(l, r - 1, dp, str) + 1;
        for (int m = l; m < r; ++m) {
            //r到m打印加上m-1到i打印
            if (str[m-1] == str[r-1]) {
                res = min(res, helper(l, m - 1, dp, str) + helper(m, r - 1, dp, str));
            }
        }
        return dp[l][r] = res;
    }
};

模拟

easy

整数反转

难度简单2799

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

1
2
输入：x = 123
输出：321

示例 2：

1
2
输入：x = -123
输出：-321

思路：将个十百千位依次读出，然后重新组成一个反转的数。

注意反转后可能溢出INT范围。

①在组成过程中，可以判断组成前的数是不是大于INT/10，大于的话，继续组下一位的时候就会溢出

②由于INT_MAX的个位是7,INT_MIN的个尾是8。

那么当x的最高位大于7并且x是与INT_MAX有相同的位数时，反转出来就会溢出。

但是这种情况在本题不存在，由于x是INT范围内的数，那么x与INT_MAX有相同的位数时，x的最高位必然只有1，2两种选择。

所以只有情况①才可能溢出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int reverse(int x) {
        int ans=0;
        while(x){
            if(ans>INT_MAX/10||ans<INT_MIN/10) //溢出
                return 0;
            ans*=10;	//腾出个位来
            ans+=x%10;	//将x的末位添加到ans
            x/=10;		//删除x的末位
        }
        return ans;
    }
};

mindium

顺时针打印矩阵

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

限制：

  • 0 <= matrix.length <= 100
  • 0 <= matrix[i].length <= 100
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> ans;
        int m=matrix.size();
        if(m==0) return ans;
        int n=matrix[0].size();
        vector<int> dir={n,m-1,n-1,m-2};//初始化第一圈要跳的步数
        int xx[]={0,1,0,-1};	//x的变化方向
        int yy[]={1,0,-1,0};	//y的变化方向
        int x=0,y=-1;	//要先从外面跳进去
        while(true){
            for(int i=0;i<4;++i){	//决定现在的方向
                if(!dir[i]) return ans;	//不需要跳了，返回答案
                for(int j=0;j<dir[i];++j){//开始跳dir[i]步
                    x+=xx[i];
                    y+=yy[i];
                    ans.emplace_back(matrix[x][y]);
                }
                dir[i]-=2;//内层每个方向要跳的步数减少二
            }
        }
    }
};

把字符串转换成整数

写一个函数 StrToInt，实现把字符串转换成整数这个功能。不能使用 atoi 或者其他类似的库函数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。

当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。

该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0。

说明：

假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围，请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。

思路：模拟遍历。

判断越界的时候利用已获得的前缀和当前数字去比较INT最大最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int strToInt(string str) {
        int i=0;
        bool isNagetive=false;
        while(str[i]==' ')i++;  //跳过前面的空格,这里不会越界,因为最后有\n
        if(str[i]=='-'){        //负数
            i++;
            isNagetive=true;
        }else if(str[i]=='+')i++;   //正数
        int ans=0;
        for(;i<str.size();++i){
            int tmp=str[i]-'0';
            if(tmp<=9&&tmp>=0){ //当前是数字
                /*现在的前缀大于最大(小)值前缀,或者现在的前缀等于最大(小)值前缀并且
                最后一位大于7的时候越界*/
                if(ans>INT_MAX/10||ans==INT_MAX/10&&tmp>7){ 
                    return isNagetive?INT_MIN:INT_MAX;
                }
                ans=ans*10+tmp;
            }else break;    //遍历到不是数字了,返回答案
        }
        return isNagetive?-ans:ans;
    }
};

树

easy

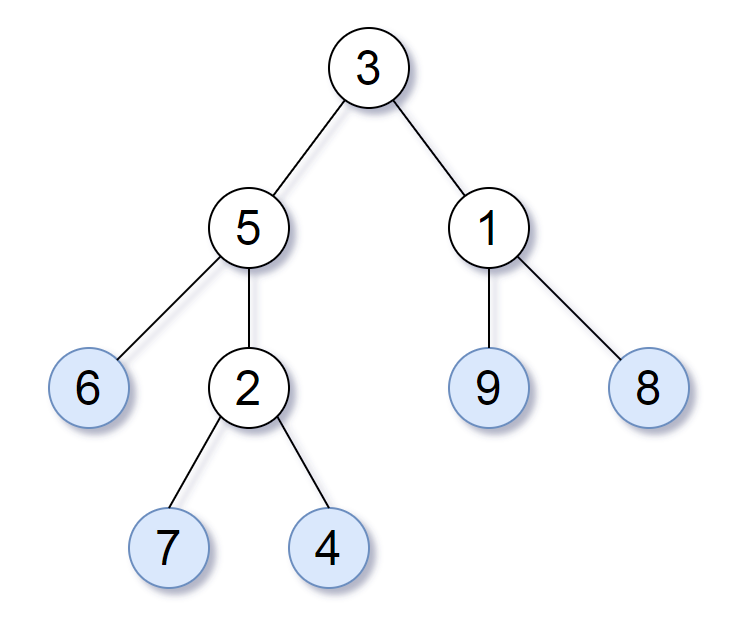
叶子相似的树

请考虑一棵二叉树上所有的叶子，这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。

img

举个例子，如上图所示，给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。

如果有两棵二叉树的叶值序列是相同，那么我们就认为它们是 叶相似 的。

如果给定的两个根结点分别为 root1 和 root2 的树是叶相似的，则返回 true；否则返回 false 。

思路：前序遍历可以按左到右遍历这些叶结点，判断是不是叶结点按顺序加入数组，判断两次得到的数组是否相同得出答案。

时间复杂度O(n+m)n,m分别为两棵树的节点数

空间复杂度O(max(k1+n1,k2+n2))k1，k2分别为两棵树最大深度,n1,n2为叶值序列长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool leafSimilar(TreeNode* root1, TreeNode* root2) {
        vector<int> v1,v2;
        preorder(root1,v1);
        preorder(root2,v2);
        return v1==v2;
    }
    void preorder(TreeNode* root,vector<int>& v){
        if(!root) return;
        preorder(root->left,v);
        if(!root->left&&!root->right)
            v.emplace_back(root->val);
        preorder(root->right,v);
    }
};

二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

img

示例 1:

1
2
3
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

思路：总体来说是找一个节点，它的左树或者右树不同时包括p,q。所以当满足p,q不同时小于左节点或p,q不同时大于右节点，该节点就是所求。

递归版：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
            if(root==NULL) 
                return NULL;
            else if(root->val<q->val&&root->val>p->val||root->val>q->val&&root->val<p->val)
                return root;
            else if(root==q||root==p)
                return root;
            TreeNode* l=lowestCommonAncestor(root->left,p,q);
            TreeNode* r=lowestCommonAncestor(root->right,p,q);
            return (l==NULL)?r:l;
    }
}

非递归版：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while(true){
            if(max(p->val,q->val)<root->val)
                root=root->left;
            else if(min(p->val,q->val)>root->val)
                root=root->right;
            else break;
        }
        return root;
    }
}

计数版：效率最低，找左子树和右子树和自己，共有多少个p,q节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    TreeNode * ans=NULL;
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        dfs(root,p,q);
        return ans;
    }
    int dfs(TreeNode* root, TreeNode*& p, TreeNode*& q) {
        if(root==NULL)return 0;
        int l= dfs(root->left,p,q);
        int r= dfs(root->right,p,q);
        int count=l+r;
        if(root==q) count++;
        if(root==p) count++;
        // cout<<root->val<<" "<<count<<endl;
        if(count==2&&ans==NULL) ans=root; 
        return count;
    }
};

平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

思路：维持一个bool值（ans），先序遍历树，返回树的最大深度，如果ans==false，直接返回，如果不为false，判断左右子树的深度是否相差大于1。大于1修改ans为false。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool ans=true;
    int dfs(TreeNode* root){
        if(!root||ans==false) return 0;
        int ldep=dfs(root->left)+1;
        int rdep=dfs(root->right)+1;
        if(abs(ldep-rdep)>1)
            ans=false;
        return max(ldep,rdep);
    }
    bool isBalanced(TreeNode* root) {
        dfs(root);
        return ans;
    }
};

medium

树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

思路：遍历找到A树所有B树根节点相同值的节点，以A树上的节点作头节点（A‘树），同时遍历A‘树和B树判断B是不是A‘的子结构。

另外的思路：bfs找A树所有B树根节点相同值的节点，再判断。

时间复杂度：O($MN$)M为A的节点数，N为B的节点数

空间复杂度：O($M$),当树 A 和树 B 都退化为链表时，递归调用深度最大。当 M ≤N 时，遍历树 A 与递归判断的总递归深度为 M ；当 M>N 时，最差情况为遍历至树 A 叶子节点，此时总递归深度为 M。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        if(!A||!B)return false;	//因为B为空不是子结构，而且A为空时，必没有子结构
        //判断A，B树是不是同根的子结构或者看看A的左子树和右子树有没有B的子结构
        return isSame(A,B)||isSubStructure(A->left,B)||isSubStructure(A->right,B);
    }
    bool isSame(TreeNode* a,TreeNode* b){
        //实际是遍历B树与A对应
        if(b==nullptr)return true;
        //当前节点相同时，继续判断左右子树
        if(a&&b&&a->val==b->val)
            return isSame(a->left,b->left)&&isSame(a->right,b->right);
        //当A先为空时，或者A与B不同时，返回false
        return false;
    }
};

超级压缩版

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        return A&&B&&(isSame(A,B)||isSubStructure(A->left,B)||isSubStructure(A->right,B));
    }
    bool isSame(TreeNode* a,TreeNode* b){
        if(!b)return true;
        if(a&&a->val==b->val)
            return isSame(a->left,b->left)&&isSame(a->right,b->right);
        return false;
    }
};

二叉树中和为某一值的路径

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

示例:
给定如下二叉树，以及目标和 target = 22，

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

返回:

1
2
3
4
5
[
   [5,4,11,2],
   [5,8,4,5]
]

思路：简单的回溯，记录路径累积值和路径，当target与累计值相同时，保存路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<vector<int>>ans;
    vector<vector<int>> pathSum(TreeNode* root, int target) {
        if(!root)return {};
        vector<int> tmp;
        dfs(root,0,target,tmp);
        return ans;
    }
    void dfs(TreeNode* root,int curval,int target,vector<int>& tmp){
        if(root->left==nullptr&&root->right==nullptr){		//叶结点
            if(target==curval+root->val){
                tmp.emplace_back(root->val);				//加入叶结点
                ans.emplace_back(tmp);						//保存路径
                tmp.pop_back();								//回溯
            }
            return ; 
        }
        tmp.emplace_back(root->val);				//加入当前结点
        if(root->left)dfs(root->left,curval+root->val,target,tmp);
        if(root->right)dfs(root->right,curval+root->val,target,tmp);
        tmp.pop_back();			//回溯
    }
};

二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

思路：中序遍历，将前一个节点的右节点指向当前遍历节点，当前遍历节点的左节点指向前一个节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        dfs(root);	中序遍历
        if(head){	//如果有链表头结点
            head->left=pre;	//链表头结点右孩子指向最后遍历的节点
            pre->right=head;//最后遍历的节点左孩子指向链表头结点
        }
        return head;
    }
private:
    //pre前一个遍历的节点，head链表头结点
    Node*pre =nullptr,*head=nullptr;
    void dfs(Node* root){
        if(!root)return ;
        dfs(root->left);
        root->left=pre;	//当前遍历节点的左节点指向前一个节点
        //前一个节点的右节点指向当前遍历节点
        //pre为空，root就是链表头结点
        if(pre)pre->right=root;
        else head=root;
        pre=root;
        dfs(root->right);
        return ;
    }
};

最小高度树

难度中等332

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

示例 1：

img

1
2
3
输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 3：

1
2
输入：n = 1, edges = []
输出：[0]

快速翻译一下题目就是选树中的一个节点当根节点，使得树有最小高度。

其实就是找树中最长路径的中点。

思路：先组成一个图，层次遍历，将连接的节点的入度减一,将所有入度1的节点入队。直到最后一层。最后一层就是答案。答案最多两个元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        vector<int> indegree(n);//入度表
        vector<vector<int>> relations(n,vector<int>());//邻接表
        for(int i=0;i<edges.size();++i){	//初始化入度表和邻接表
            relations[edges[i][1]].emplace_back(edges[i][0]);
            relations[edges[i][0]].emplace_back(edges[i][1]);
            ++indegree[edges[i][0]];
            ++indegree[edges[i][1]];
        }
        queue<int> que;
        for(int i=0;i<indegree.size();++i){//将入度为1的节点入队
            if(indegree[i]<=1)//注意这里包含了一个节点的树
                que.push(i);
        }
        vector<int> ans;
        while(!que.empty()){
            int levelsize=que.size();
            ans.clear();//清空上一层的结果
            while(levelsize--){  //层次遍历
                int tmp=que.front();
                que.pop();
                ans.emplace_back(tmp);		//记录本层
                for(int i=0;i<relations[tmp].size();++i){//tmp连接的节点的入度减一
                    --indegree[relations[tmp][i]];
                    if(indegree[relations[tmp][i]]==1){
                        que.push(relations[tmp][i]);
                    }
                }
            }
        }
        return ans;
    }
};

二叉搜索树中第K小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

中序遍历加剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int count=0;
    int K;
    int ans=0;
    int kthSmallest(TreeNode* root, int k) {
        K=k;
        slove(root);
        return ans;
    }
    void slove(TreeNode* root) {
        if(root&&count!=K){
            slove(root->left);
            if(++count==K){
                ans=root->val;
                return ;
            }
            slove(root->right);
        }
    }
};

hard

二叉树中的最大路径和

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

思路：每个节点root设定一个贡献值，该贡献值为含义为：root的子树的路径的最大路径和，并且这个路径的端点为root。

也就是在该节点的子树下找一条路径，满足以下两个条件

路径的一个端点必须是该节点

这条路径的路径和最大

这条路径的路径和就是贡献值。

那么在cur节点，可以知道，是否要选左路径或者右路径或者两个都不选，

通过他们的贡献值而定，如果路径贡献值为负数，但就不选。

左右路径都为负，那就只有cur节点作为一个路径。

设定一个ans变量储存最大值，只要遍历所有的节点，就可以记录下来所有的子树最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int ans=INT_MIN;
    int dfs(TreeNode* root){
        if(root == nullptr)		//空树贡献值为0
            return 0;
        int leftval = max(dfs(root -> left), 0);//选不选左子树
        int rightval = max(dfs(root -> right), 0);//选不选右子树
        //当前树的最大值跟历史最大值比较
        ans = max(ans, leftval + rightval + root -> val);
        //返回贡献值，注意要保持root是端点，所以只能选左右子树其中最大的路径
        return root -> val + max(leftval, rightval);
    }
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return ans;
    }
};

数组

hard

寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

示例 1：

1
2
3
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

思路：找出两个数组中第k小的数来代替找中位数。（两个数组长度总和为偶数则找第k和k+1个数，否则找第k+1个数（k=(len1+len2)/2））。

这里两个数组找第k小的元素的方法是：

从数组1找从index1开始第k/2个的数。

从数组2找从index2开始第k/2个的数。

比较大小，小于等于的那一行的可以排除是第k小的可能性。（因为它最多大于k-2个元素）

怎么排除？

修改相应index（index1，index2）index修改为newindex+1，还有k要减去减去元素的数量。

一直遍历，会出现2种情况。

情况1：找完了其中一个数组，还没找到第k小元素。也就是其中有一个数组所有元素都比第k小元素小。

这时候直接找长数组的index+k个元素就是所求。

情况2：k==1，说明找到了，直接拿最小的index的数。（这里肯定会剩一个以上，因为只会排除小于等于的那一行，另一行必然剩一个以上）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int getKthnum(vector<int>& nums1, vector<int>& nums2,int k){
        int n=nums1.size()-1;
        int m=nums2.size()-1;
        int index1=0;
        int index2=0;
        while(true){
            if(index1==n+1)
                return nums2[index2+k-1];
            if(index2==m+1)
                return nums1[index1+k-1];
            if(k==1)
                return min(nums1[index1],nums2[index2]);
            int newindex1=min(n,index1+k/2-1);
            int newindex2=min(m,index2+k/2-1);
            if(nums1[newindex1]>=nums2[newindex2]){
                k-=newindex2-index2+1;
                index2=newindex2+1;
            }else{
                k-=newindex1-index1+1;
                index1=newindex1+1;
            }
        }
    }
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int count=nums1.size()+nums2.size();
        if(count%2)
            return getKthnum(nums1,nums2,count/2+1);
        else{
            return (getKthnum(nums1,nums2,count/2)+getKthnum(nums1,nums2,count/2+1))/2.0;
        }
    }
};

数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

1
2
输入: [7,5,6,4]
输出: 5

思路1：在归并排序的过程中记录有多少逆序对。

num1 num2 nums 逆序对数
[9, 26, 55, 64, 91] [8, 12, 16, 22, 100] [] 0
[9, 26, 55, 64, 91] [12, 16, 22, 100] [8] 0+nums1.size()=5
[26, 55, 64, 91] [12, 16, 22, 100] [8,9] 5
[26, 55, 64, 91] [16, 22, 100] [8,9,12] 5+nums1.size()=9
[26, 55, 64, 91] [22, 100] [8,9,12,16] 9+num1.size()=13
[26, 55, 64, 91] [100] [8,9,12,16,22] 13+=num1.size()=17
[55, 64, 91] [100] [8,9,12,16,22,26] 17
[64, 91] [100] [8,9,12,16,22,26,55] 17
[91] [100] [8,9,12,16,22,26,55,64] 17
[] [100] [8,9,12,16,22,26,55,64,91] 17
[] [] [8,9,12,16,22,26,55,64,91,100] 17+num1.size()=17 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int reversePairs(vector<int>& nums) {
        vector<int> tmp(nums.size());		//辅助数组
        return getPairscount(nums,tmp,0,nums.size()-1);
    }
    int getPairscount(vector<int>& nums,vector<int>& tmp,int left,int right){
        if(left>=right) return 0;
        int mid=left+(right-left)/2;
        int lcount=getPairscount(nums,tmp,left,mid);	//获取左区间逆序对数
        int rcount=getPairscount(nums,tmp,mid+1,right);	//获取右区间逆序对数
        int count =merge(nums,tmp,left,mid,right);		//合并当前区间的逆序对数
        return lcount+rcount+count;
    }
    int merge(vector<int>& nums,vector<int>& tmp,int left,int mid,int right){
        int count=0;
        int index=left,start1=left,start2=mid+1,end1=mid,end2=right;
        while(index<=right){
            if(start1==end1+1)
                tmp[index++]=nums[start2++];
            else if(start2==end2+1||nums[start1]<=nums[start2]){
                tmp[index++]=nums[start1++];
            }else{
                tmp[index++]=nums[start2++];
                count+=end1-start1+1;		//将num1剩余的元素个数加入count
            }
        }
        copy(tmp.begin()+left,tmp.begin()+right+1,nums.begin()+left);
        return count;
    }
};

二分查找

medium

制作 m 束花所需的最少天数

给你一个整数数组 bloomDay，以及两个整数 m 和 k 。

现需要制作 m 束花。制作花束时，需要使用花园中 相邻的 k 朵花 。

花园中有 n 朵花，第 i 朵花会在 bloomDay[i] 时盛开，恰好 可以用于 一束 花中。

请你返回从花园中摘 m 束花需要等待的最少的天数。如果不能摘到 m 束花则返回 -1 。

思路：对bloomDay数组范围二分，寻找满足条件的一个天数。

注意找到可行解后，可能还有更优解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int minDays(vector<int>& bloomDay, int m, int k) {
        int right=*max_element(bloomDay.begin(),bloomDay.end());
        int left=*min_element(bloomDay.begin(),bloomDay.end());
        int ans=-1;
        while(left<=right){
            int mid=left+(right-left)/2;
            int bloomcount=0,conbloom=0;
            for(int i=0;i<bloomDay.size();++i){
                if(bloomDay[i]<=mid){
                    ++conbloom;
                    if(conbloom==k){
                        conbloom=0;
                        ++bloomcount;
                    }
                }else{
                    conbloom=0;
                }
            }
            if(bloomcount>=m){
                ans=mid;
                right=mid-1;
            }else if(bloomcount<m){
                left=mid+1;
            }else{
                right=mid-1;
            }
        }
        return ans;
    }
};

回文

easy

回文数

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。

回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。例如，121 是回文，而 123 不是。

示例 1：

1
2
输入：x = 121
输出：true

示例 2：

1
2
输入：x = -121
输出：false

思路1：先转字符串，然后前后判断。

思路2：把后面一半的数拿出来倒过来组成新的数，看看是不是与前面半段相等。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool isPalindrome(int x) {
        if(x<0||x%10==0&&x!=0)return false;//非0的末尾位是0的数和负数
        string str=to_string(x);
        int l=0,r=str.size()-1;
        for(;l<r;++l,--r){
            if(str[l]!=str[r])
                return false;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool isPalindrome(int x) {
        if(x<0||x%10==0&&x!=0)return false;
        int reverseNum=0;
        while(reverseNum<x){		//一直判断到中间
            reverseNum*=10;			//先空出个位
            reverseNum+=x%10;		//取x的最后一位
            x/=10;					//去掉x最后一位
        }
        return reverseNum==x||(reverseNum/10==x);//偶数和单数个数字
    }
};

验证回文串

给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。

说明：本题中，我们将空字符串定义为有效的回文串。

示例 1:

1
2
输入: "A man, a plan, a canal: Panama"
输出: true

思路1：直接存反转后的判断二者是不是相等。

时间复杂度O（N）

空间复杂度O（N）

思路2：双指针

双指针放在前后，往中间判断，不同就返回false。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    bool isPalindrome(string s) {
       string alnumstr="";
       for(auto ch:s){
           if(isalnum(ch))
                alnumstr+=toupper(ch);
       }
    /* string str_rev=alnumstr;    
     * reverse(str_rev.begin(),str_rev.end());  //反转
     */
        string str_rev(alnumstr.rbegin(), alnumstr.rend()); //反转
        return str_rev==alnumstr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool isPalindrome(string s) {
        int l=0,r=s.size()-1;
        while(l<r){
            while(l<r&&!isalnum(s[l]))++l;
            while(l<r&&!isalnum(s[r]))--r;
            if(l<r){
                if(toupper(s[l])!=toupper(s[r]))
                    return false;
                l++;
                r--;
            }
        }
        return true;
    }
};

异或

medium

解码异或后的排列

给你一个整数数组 perm ，它是前 n 个正整数的排列，且 n 是个 奇数 。

它被加密成另一个长度为 n - 1 的整数数组 encoded ，满足 encoded[i] = perm[i] XOR perm[i + 1] 。比方说，如果 perm = [1,3,2] ，那么 encoded = [2,1] 。

给你 encoded 数组，请你返回原始数组 perm 。题目保证答案存在且唯一。

示例 1：

1
2
3
输入：encoded = [3,1]
输出：[1,2,3]
解释：如果 perm = [1,2,3] ，那么 encoded = [1 XOR 2,2 XOR 3] = [3,1]

思路：先求出1-n的异或allxor。allxor=encoded[0]^encoded[1]^encoded[2]····^encoded[n-1] ①

perm[0]=encoded[0]^encoded[1]

perm[1]=encoded[1]^encoded[2] ②

perm[3]=encoded[3]^encoded[4] ③

perm[5]=encoded[5]^encoded[6] ④

将②③④等奇数序号perm代入①得

allxor=encoded[0]^perm[1]^perm[3]^perm[5]·······

求出xor1toN=perm[1]^perm[3]^perm[5]·······

那么encoded[0]=xor1toN^allxor

由encoded[0]^encoded[1]=perm[0]得

encoded[1]=encoded[0]^perm[0]。

如此类推。

注意前1-n的异或可以O（1）得出

1
2
3
4
5
6
switch(n%4){
           case 0:allxor=n+1;break;
           case 1:allxor=1;  break;
           case 2:allxor=n+2;break;
           case 3:allxor=0;  break;
       }

拓展：同理 k-n的连续异或(knxor)也可以由1-k的异或(kxor)和1-n(nxor)的异或求出。

knxor=kxor^nxor

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> decode(vector<int>& encoded) {
        int allxor=0;
        // for(int i=1;i<=encoded.size()+1;i++)
        //     allxor^=i;

        int n=encoded.size()+1;
        switch(n%4){
            case 0:allxor=n+1;break;
            case 1:allxor=1;  break;
            case 2:allxor=n+2;break;
            case 3:allxor=0;  break;
        }
      
        int xor1toN=0;
        for(int i=1;i<encoded.size();i+=2)
            xor1toN^=encoded[i];
        vector<int> ans;
        int tmp=allxor^xor1toN;
        ans.emplace_back(tmp);
        for(int x:encoded)
            ans.emplace_back(tmp^=x);
        return ans;
    }
};

找出第 K 大的异或坐标值

给你一个二维矩阵 matrix 和一个整数 k ，矩阵大小为 m x n 由非负整数组成。

矩阵中坐标 (a, b) 的 值 可由对所有满足 0 <= i <= a < m 且 0 <= j <= b < n 的元素 matrix[i][j]（下标从 0 开始计数）执行异或运算得到。

请你找出 matrix 的所有坐标中第 k 大的值（k 的值从 1 开始计数）。

示例 1：

1
2
3
输入：matrix = [[5,2],[1,6]], k = 1
输出：7
解释：坐标 (0,1) 的值是 5 XOR 2 = 7 ，为最大的值。

思路：要求异或坐标值需要左上角所有的元素（包括自己的行和列和自己）异或和。要求matrix [i] [j]时matrix [i-1] [j-1]和matrix [i-1] [j]和matrix [i] [j-1]都已经求得，而matrix [i] [j-1]和matrix [i-1] [j]区域重合了matrix [i-1] [j-1]的区域，所以要求matrix [i] [j]需要补上matrix [i-1] [j-1]区域所以得出

1
matrix[i][j]=matrix[i][j]^matrix[i-1][j]^matrix[i][j-1]^matrix[i][j]

然后就是求出第k大元素，用堆(nmlogk)或者快速选择算法（nm，最坏nm^2），或者排序（nmlognm）都可以。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int kthLargestValue(vector<vector<int>>& matrix, int k) {
        int m=matrix.size();
        int n=matrix[0].size();
        vector<int> helper;
        helper.emplace_back(matrix[0][0]);
        for(int i=1;i<m;++i){		//求第一列
            matrix[i][0]=matrix[i][0]^matrix[i-1][0];
            helper.emplace_back(matrix[i][0]);
        }
        for(int i=1;i<n;++i){		//求第一行
            matrix[0][i]=matrix[0][i]^matrix[0][i-1];
            helper.emplace_back(matrix[0][i]);
        }
        for(int i=1;i<m;++i){
            for(int j=1;j<n;++j){
                matrix[i][j]^=matrix[i-1][j]^matrix[i][j-1]^matrix[i-1][j-1];
                helper.emplace_back(matrix[i][j]);
            }
        }
        nth_element(helper.begin(),helper.begin()+k-1,helper.end(),greater<int>());
        return helper[k-1];
    }
};

hard

与数组中元素的最大异或值

给你一个由非负整数组成的数组 nums 。另有一个查询数组 queries ，其中 queries[i] = [xi, mi] 。

第 i 个查询的答案是 xi 和任何 nums 数组中不超过 mi 的元素按位异或（XOR）得到的最大值。换句话说，答案是 max(nums[j] XOR xi) ，其中所有 j 均满足 nums[j] <= mi 。如果 nums 中的所有元素都大于 mi，最终答案就是 -1 。

返回一个整数数组 answer 作为查询的答案，其中 answer.length == queries.length 且 answer[i] 是第 i 个查询的答案。

思路：用nums中元素二进制构建前缀树，在前缀树中尽可能的找最大异或值，每个节点存放该子树和自身的最小值，寻找的时候需要兼顾找最大异或和保持不大于mi（这个更优先）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class Solution {
public:
    struct inode{
        int minsonval=INT_MAX;	//该子树和自身的最小值
        int index;	//如果是叶结点，就存放元素在nums的序号
        inode* zero,* one;		//子节点
    };
    class prefixtree{
    private:
        inode* head;
    public:
        prefixtree(){
            head=new inode();
        }
        void insertNode(vector<int>& nums,int index){	//插入nums[index]
            inode* cur=head;
            for(int i=30;i>=0;--i){
                int tmp=(nums[index]/(1<<i))&1;		//从最高位依次取位
                if(tmp==1){		//建树
                    if(!cur->one)cur->one=new inode();
                    cur->minsonval=min(cur->minsonval,nums[index]);
                    cur=cur->one;
                }else{
                    if(!cur->zero)cur->zero=new inode();
                    cur->minsonval=min(cur->minsonval,nums[index]);
                    cur=cur->zero;
                }
            }
            cur->minsonval=nums[index]; //cur==叶结点
            cur->index=index;	//存放序号
        }
        //找x和nums中小于m的元素异或的最大值
        int searchMAXXOR(vector<int>& nums,int x,int m){
            inode* cur=head;
            for(int i=30;i>=0;--i){
                int tmp=(x/(1<<i))&1;//x从最高位依次取位
                inode* tmpcur=cur;	//保存cur指针
                if(tmp==1){
                    //先判断是否为空，再判断是否小于m,优先看与tmp相反的zero，下同
                    if(cur->zero&&cur->zero->minsonval<=m) cur=cur->zero;
                    else if(cur->one&&cur->one->minsonval<=m)cur=cur->one;
                }else{
                     if(cur->one&&cur->one->minsonval<=m)cur=cur->one;
                     else if(cur->zero&&cur->zero->minsonval<=m) cur=cur->zero;
                }
                if(cur==tmpcur) return -1;	//cur没有改变，说明没有满足小于m的数
            }
            return nums[cur->index]^x;	//到了叶结点
        }
    };
    vector<int> maximizeXor(vector<int>& nums, vector<vector<int>>& queries) {
        prefixtree tree;
        vector<int> ans;
        for(int i=0;i<nums.size();++i)
            tree.insertNode(nums,i);
        for(vector<int> query:queries)
            ans.emplace_back(tree.searchMAXXOR(nums,query[0],query[1]));
        return ans;
    }
};

字典树

medium

数组中两个数的最大异或值

给你一个整数数组 nums ，返回 nums[i] XOR nums[j] 的最大运算结果，其中 0 ≤ i ≤ j < n 。

进阶：你可以在 O(n) 的时间解决这个问题吗？

示例 1：

1
2
3
输入：nums = [3,10,5,25,2,8]
输出：28
解释：最大运算结果是 5 XOR 25 = 28.

思路：由于题目是选两个数异或，而且还可以选自己跟自己异或所以下界是0。

本题可以使用字典树（前缀树）来做。

将每个数字转成字符串然后从最高位开始存。

构造一个32位树高的前缀树(含一个头节点)。

然后遍历数组想办法从树里找到尽可能每一位跟当前遍历到的数（x）相反的数(y)。

比如101要尽力去找010。

然后比较每一个x^y,找出最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Solution {
public:
    struct node{	//树的节点
        int index=-1;	//叶结点会存放在nums数组的序号
        node* zero;
        node* one;
    };
    class prefixTree{
    private:
        node* top;	//头结点
    public:
        prefixTree(){
            top=new node();
        }
        void add(int num,int index){//num加入前缀树，index是num在nums的序号
            node* cur=top;			//当前处理的节点
            for(int i=30;i>=0;i--){	.//从最高位开始找
                int tmp=(num>>i)&1;	//找到第i位的数  0或者1
                if(tmp==1){
                    if(!cur->one)cur->one=new node();	//没有就构造,下面同理
                    cur=cur->one;		//更新cur
                }else{
                    if(!cur->zero)cur->zero=new node();
                    cur=cur->zero;
                }
            }
            cur->index=index;	//叶结点存放num在nums的序号。
        }
        int findMAXXORnum(int num){	//找到树里尽量每一位和num相反的数
            node* cur=top;			//当前处理的节点
            for(int i=30;i>=0;i--){
                int tmp=(num>>i)&1;		//找到num第i位的数  0或者1
                if(!cur->one&&!cur->zero)	//叶结点返回找到的数在nums的序号
                    return cur->index;
                if(tmp==1){			//1的话转到0
                    if(cur->zero) cur=cur->zero; 
                    else cur=cur->one;	//没有0只能转1
                }else{				//0的话转到1
                    if(cur->one)cur=cur->one;
                    else cur=cur->zero;	//没有1只能转0
                }
            }
            return cur->index;	//叶结点返回找到的数在nums的序号
        }
    };

    int findMaximumXOR(vector<int>& nums) {
        prefixTree tree;
        for(int i=0;i<nums.size();i++)	//将nums全部加入前缀树
            tree.add(nums[i],i);
        int ans=0;		//下界是0
        for(auto num:nums){
            int index=tree.findMAXXORnum(num);//找到树里尽量每一位和num相反的数
            ans=max(ans,nums[index]^num);
        }
        return ans;
    }
};

思路2：int31位。从最高位开始找，如果可以设置为1就设置为1。

怎么判断可以设置1？

set存放数组里所有数的前K位。示例：xxxxx?????存放xxxxx

首先先设置为1

可以得到xxxx1????(前面是已经找到的最优解)截取前面的得到xxxx1

数组里其他截取前面的得到abcde

二者相与得到一个fghij，如果fghij在set中说明设置1是可行的。

不然只能设置为0

然后继续判断下一位。

为什么fghij在set中就说明设置1是可行的？

因为前面的fghi也可以在前k-1位set也可以找到。

由此类推。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int findMaximumXOR(vector<int>& nums) {
        int ans=0;
        for(int i=30;i>=0;i--){
            unordered_set<int> st;	//存放nums中的每一个元素的前30-i位。
            for(auto num:nums){
                st.insert(num>>i);
            }
            int tmp_ans=ans*2+1;	//先设置为1
            bool flag=0;
            for(int num:nums){
                if(st.count(tmp_ans^(num>>i))){		//找到了
                    flag=1;
                    break;
                }
            }
            if(flag) ans = tmp_ans;
            else ans = tmp_ans - 1;			//没找到就取消设置为1
        }
        return ans;
    }
};

回溯

medium

全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

思路：简单的回溯，依次确定第i位的可能值。确定到最后一位就是一种解。

时间复杂度O（nn!）

空间复杂度O（n）除了答案数组以外。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
private:
    vector<vector<int>> ans;
    int len;
public:
    vector<vector<int>> permute(vector<int>& nums) {
        len=nums.size();
        slove(nums,0);
        return ans;
    }
    void slove(vector<int>& nums,int i){
        if(len-1==i){		//判断到了最后一位
            ans.emplace_back(nums);
        }
        for(int j=i;j<len;++j){
            swap(nums[i],nums[j]);	//将选中的后面的位跟现在i位交换
            slove(nums,i+1);		//找i+1位后的全排列
            swap(nums[i],nums[j]);	//交换回去
        }
    }
};

矩阵中的路径

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

思路：dfs搜索路径是否等于word，加入剪枝。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
private:
    int dx[4]{0,1,-1,0};//方向数组
    int dy[4]{-1,0,0,1};
    int colsize=0,rowsize=0; 	//行列数
    bool dfs(vector<vector<char>>& board,string& word,int x,int y,int dep){
        //不满足条件的返回false
        if(x>=rowsize||x<0||y>=colsize||y<0||board[x][y]!=word[dep])
            return false;
        //已经深搜到最后一个字母，并且满足条件board[x][y]=word[dep]
        if(dep==word.size()-1)
            return true;
        board[x][y]='\n';	//把现在走过的字母先修改成不可能的字符
        for(int i=0;i<4;i++){
            if(dfs(board,word,x+dx[i],y+dy[i],dep+1)){//找到一条就返回
                return true;
            }
        }
        board[x][y]=word[dep];	//把字母恢复，给其他路径走
        return false;	//找不到路径
    }
public:
    bool exist(vector<vector<char>>& board, string word) {
        rowsize=board.size();
        colsize=board[0].size();
        for(int i=0;i<rowsize;++i){
            for(int j=0;j<board[0].size();++j){
                if(dfs(board,word,i,j,0)){
                    return true;
                }
            }
        }
        return false;
    }
};

层次遍历

medium

二叉树的锯齿形层序遍历

给定一个二叉树，返回其节点值的锯齿形层序遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如：
给定二叉树 [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回锯齿形层序遍历如下：

1
2
3
4
5
[
  [3],
  [20,9],
  [15,7]
]

思路：进行普通的层次遍历，将每层结果存在deque，若需要倒序的层，则头插，不然就尾插。然后类型转到vector，

空间复杂度O（n）n为树节点个数

时间复杂度O（n）

提交答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        queue<TreeNode *> que;
        vector<vector<int>> ans;
        if(!root) return ans;
        que.push(root); 
        int dep = 1;
        while(!que.empty()){
            int len = que.size();
            deque<int> valque;
            for(int i=0;i<len;i++){
                TreeNode* tmp = que.front();
                que.pop();
                if(dep%2) //该层不需要反转
                    valque.push_back(tmp->val);
                else	////该层需要反转
                    valque.push_front(tmp->val);
                if(tmp->left)
                    que.push(tmp->left);
                if(tmp->right)
                    que.push(tmp->right);
            }
            dep++;
            ans.emplace_back(vector<int>{valque.begin(),valque.end()});
        }
        return ans;
    }
};

思路2：将节点存在deque，下一层需反转的，取队头，然后子节点放在队尾，先放左节点，后放右节点。

下一层不需翻转的，取队尾，子节点插队头，先放右节点，再放左节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        deque<TreeNode*>que;
        vector<vector<int>> ans;
        if(!root)return ans;
        que.push_back(root);
        while(!que.empty()){
            vector<int> tmpv1;
            int len=que.size();
            for(int i=0;i<len;i++){
                TreeNode* tmp=que.front();
                que.pop_front();
                tmpv1.emplace_back(tmp->val);
                if(tmp->left)que.push_back(tmp->left);
                if(tmp->right)que.push_back(tmp->right);
            }
            ans.push_back(tmpv1);
            if(que.empty())break;
            vector<int> tmpv2;
            len=que.size();
            for(int i=len;i>0;i--){
                TreeNode* tmp=que.back();
                que.pop_back();
                tmpv2.emplace_back(tmp->val);
                if(tmp->right)que.push_front(tmp->right);
                if(tmp->left)que.push_front(tmp->left);
            }
            ans.push_back(tmpv2);
        }
        return ans;
    }
};

机器人的运动范围

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0]的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：

1
2
输入：m = 2, n = 3, k = 1
输出：3

思路：层次遍历，满足条件的可以前进，可以优化前进方向为向右或向下。

时间复杂度O($mn$)

空间复杂度O($mn$)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int getsum(int x){
        int ans=0;
        while(x){
            ans+=x%10;
            x/=10;
        }
        return ans;
    }
    int movingCount(int m, int n, int k) {
        int ans=1;
        vector<vector<bool>> isvisit(m,vector<bool>(n,false));
        queue<pair<int,int>> que;//分别表示x,y
        que.push({0,0});
        int dx[2]{0,1};//方向数组
        int dy[2]{1,0};
        isvisit[0][0]=true;
        while(!que.empty()){
            auto tmp=que.front();
            que.pop();
            for(int i=0;i<2;i++){
                int xx=tmp.first+dx[i];
                int yy=tmp.second+dy[i];
                if(xx>=0&&xx<m&&yy>=0&&yy<n&&!isvisit[xx][yy]&&getsum(xx)+getsum(yy)<=k){
                    isvisit[xx][yy]=true;
                    que.push(make_pair(xx,yy));
                    ans++;
                }
            }
        }
        return ans;
    }
};

课程表 II

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。

可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。

思路1：bfs，将所有入度为0的节点放入队列开始广搜，每次将当前节点连接到的节点入度减一，将连接到的节点入度为0的放入队列。在环里的节点将不会被搜到。所以广搜结束后，看是不是所有节点都被搜到就是答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<int> ans;
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<int> indegree(numCourses);		//入度表
        vector<vector<int>> edges(numCourses,vector<int>());//邻接表
        for(auto x:prerequisites){	//初始化入度表和邻接表
            indegree[x[0]]++;
            edges[x[1]].emplace_back(x[0]);
        }
        queue<int> que;
        for(int i=0;i<indegree.size();++i){//入度为0的节点加入队列
            if(indegree[i]==0)
                que.push(i);
        }   
        while(!que.empty()){
            int tmp=que.front();
            que.pop();
            ans.emplace_back(tmp);//取队头放入答案数组
            for(int i=0;i<edges[tmp].size();++i){
                --indegree[edges[tmp][i]];	 	//连接到的节点入度减一
                if(indegree[edges[tmp][i]]==0){	//连接到的节点入度为0的放入队列
                    que.push(edges[tmp][i]);
                }
            }
        }
        if(ans.size()!=numCourses)
            return {};
        return ans;
    }
}

思路2：dfs 随意选择一个未遍历节点，深搜。将经历的节点状态设为1，如果再次经历相同的节点，说明有环，不可能完成所有课程。深搜到底部开始回溯，并将回溯的节点设为状态2，声明他是已完成的节点。不断选择未遍历节点，直到找到环，或者全部节点都为状态2，深搜结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    vector<int> ans;
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> relation(numCourses,vector<int>());
        vector<int> status(numCourses);	//状态数组
        for(int i=0;i<prerequisites.size();++i){	//建立邻接表
            relation[prerequisites[i][1]].push_back(prerequisites[i][0]);
        }
        for(int i=0;i<numCourses;++i){
            if(status[i]==0){				//找一个未遍历节点
                if(dfs(relation,status,i))	//返回true说明有环
                    return {};
            }
        }
        reverse(ans.begin(),ans.end());
        return ans;
    }
    bool dfs(vector<vector<int>>& relation,vector<int>& status,int cur){
        if(ans.size()==status.size())	//找到所有的节点了
            return false;
        status[cur]=1;	//设置当前节点状态为1
        for(int i=0;i<relation[cur].size();++i){	//找当前节点连接的节点
            if(status[relation[cur][i]]==1)	//连接的节点状态为1，说明在前面搜到过，有环
                return true;
            else if(status[relation[cur][i]]==2)//连接的节点已经完成学习了，继续下一个
                continue;
            if(dfs(relation,status,relation[cur][i]))//继续深搜，返回true说明有环
                return true;
        }
        status[cur]=2;		//当前节点完成了
        ans.push_back(cur);	//放入栈中
        return false;		//当前节点没找到环，返回false
    }
};

环形回路

medium

环形链表 II

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。

进阶：

  • 你是否可以使用 O(1) 空间解决此题？

示例 1：

img

1
2
3
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

判断链表是否有环，用快慢指针。

图

$a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)$

当n=1时a=c

所以在快慢指针相遇时，新建一个头指针，慢指针和新指针同时走相同的步数时，会在入口处相遇

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast=head;//head指针充当慢指针
        ListNode* ans=head;//新指针
        while(fast&&fast->next){	//fast指针判空，由于链表数奇偶的关系，需要判断next和fast，这里退出说明无环
            fast=fast->next->next;
            head=head->next;
            if(head==fast){				//slow和fast相遇
                while(ans!=head){		//slow和新指针同步向前直到相遇
                    head=head->next;
                    ans=ans->next;
                }
                return ans;
            }
        }
        return nullptr;
    }
};

字符串处理

esay

翻转单词顺序

输入一个英文句子，翻转句子中单词的顺序，但单词内字符的顺序不变。为简单起见，标点符号和普通字母一样处理。例如输入字符串”I am a student. “，则输出”student. a am I”。

示例 1：

1
2
输入: "the sky is blue"
输出: "blue is sky the"

示例 2：

1
2
3
输入: "  hello world!  "
输出: "world! hello"
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

示例 3：

1
2
3
输入: "a good   example"
输出: "example good a"
解释: 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

思路：先全部翻转，然后把每一个单词翻转，然后去掉前面和后面的所有空格和中间的多余空格。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    string reverseWords(string s) {
        reverse(s.begin(),s.end());	//全部翻转
        int left=0,right=0;
        while(right<s.size()){
            while(s[left]==' ')	//跳过空格
                ++left;
            right=left;
            while(right<s.size()&&s[right]!=' ')//到单词的末尾或者字符末尾
                ++right;
            reverse(s.begin()+left,s.begin()+right);//翻转这个单词
            ++right;	//到下一个位置
            left=right;
        }
        string ans;
        int count=0;
        left=0;
        right=s.size()-1;
        while(s[left]==' ')//找最前面不是空格的，这里由于空串s[0]=='\n'所有不用判断越界
            ++left;
        while(right>=0&&s[right]==' ')//找最后面不是空格的字母
            --right;
        for(int j=left;j<=right;++j){
            if(s[j]==' '){
                if(!count)	//第一次遇到空格
                    ans.push_back(s[j]);
                ++count;
            }else {
                count=0;	//遇到非空格清0
                ans.push_back(s[j]);
            }
        }
        return ans;
    }
};

字符串相加

给定两个字符串形式的非负整数 num1 和 num2 ，计算它们的和。

提示：

  1. num1 和 num2 的长度都小于 5100
  2. num1 和 num2 都只包含数字 0-9
  3. num1 和 num2 都不包含任何前导零
  4. 你不能使用任何內建 BigInteger 库， 也不能直接将输入的字符串转换为整数形式

思路：将num2加到num1上，模拟加法，双指针指向两个字符串尾部，往前加，维持一个变量pre表示进位。

边界处理：

保证num1长度大于等于num2,注意加完num2可能还有进位。

可能结果大于num1的长度，即最后有进位。举例：99+1=100

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    string addStrings(string num1, string num2) {
        if(num2.size()>num1.size())//保证num1长度大于等于num2
            num1.swap(num2);
        //index为指针，指向最后一位数，注意有换行符
        int index1=num1.size()-1;
        int pre=0,tmp;
        for(int index2=num2.size()-1;index1>=0;index1--,index2--){
            if(index2>=0)		//处理num1，num2都有的情况
                tmp=num1[index1]-'0'+num2[index2]-'0'+pre;
            else{				//只剩num1
                if(!pre)break;	//没有进位了可以退出
                tmp=num1[index1]-'0'+pre;
            }
            num1[index1]=tmp%10+'0';
            pre=tmp/10;	//确定是否有进位
        }
        if(pre) num1.insert(num1.begin(),'1') ;//最后一位没进，补上1在前面
        return num1;
    }
};

前缀和

medium

和为K的子数组

给定一个整数数组和一个整数 k，你需要找到该数组中和为 k 的连续的子数组的个数。

示例 1 :

1
2
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。

本题和和为s的连续正数序列类似但不同，不同之处在于递增序列和含有负数。所以不能用滑动窗口

思路与两数之和类似，不过添加了前缀和的知识。

哈希表mp[前缀和]=前缀和的数目

这样区间[i,j]=j-1的前缀和减去i的前缀和

首先求出当前i+1前缀和sum，然后看哈希表里是否有k-sum(这时哈希表存放了0到j的前缀和)，有就将前缀和数量加到ans

将当前前缀和插插入mp。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int,int> mp;
        int sum=0,ans=0;
        mp[0]=1;
        for(int i=0;i<nums.size();++i){
            sum+=nums[i];		//求出当前i+1前缀和sum
            if(mp.find(sum-k)!=mp.end())//哈希表存放了0到i的前缀和
                ans+=mp[sum-k];
            mp[sum]++;	//将i+1的前缀和加入
        }
        return ans;
    }
};

hard

元素和为目标值的子矩阵数量

给出矩阵 matrix 和目标值 target，返回元素总和等于目标值的非空子矩阵的数量。

子矩阵 x1, y1, x2, y2 是满足 x1 <= x <= x2 且 y1 <= y <= y2 的所有单元 matrix[x][y] 的集合。

如果 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 两个子矩阵中部分坐标不同（如：x1 != x1'），那么这两个子矩阵也不同。

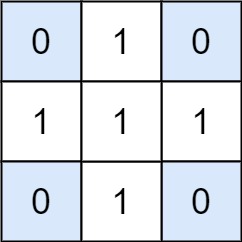
示例 1：

img

1
2
3
输入：matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
输出：4
解释：四个只含 0 的 1x1 子矩阵。

思路：外层跟最大子矩阵的思路类似，双层循环遍历确定上下边界，压缩为一维数组，然后根据和为k的子数组思路，找出子数组的个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
        vector<int> count(matrix[0].size());
        int ans=0;
        for(int i=0;i<matrix.size();++i){
            fill(count.begin(),count.end(),0);//换上边界，清空
            for(int j=i;j<matrix.size();++j){//下边界
                unordered_map<int,int> mp;
                int sum=0;
                mp[0]=1;
                for(int k=0;k<matrix[0].size();++k){
                    count[k]+=matrix[j][k];		//累积本层的数
                    sum+=count[k];				//前缀和
                    if(mp.find(sum-target)!=mp.end())
                        ans+=mp[sum-target];
                    mp[sum]++;
                }
            }
        }
        return ans;
    }
};

贪心

hard

课程表 III

这里有 n 门不同的在线课程，他们按从 1 到 n 编号。每一门课程有一定的持续上课时间（课程时间）t 以及关闭时间第 d 天。一门课要持续学习 t 天直到第 d 天时要完成，你将会从第 1 天开始。

给出 n 个在线课程用 (t, d) 对表示。你的任务是找出最多可以修几门课。

示例：

1
2
3
4
5
6
7
8
输入: [[100, 200], [200, 1300], [1000, 1250], [2000, 3200]]
输出: 3
解释: 
这里一共有 4 门课程, 但是你最多可以修 3 门:
首先, 修第一门课时, 它要耗费 100 天，你会在第 100 天完成, 在第 101 天准备下门课。
第二, 修第三门课时, 它会耗费 1000 天，所以你将在第 1100 天的时候完成它, 以及在第 1101 天开始准备下门课程。
第三, 修第二门课时, 它会耗时 200 天，所以你将会在第 1300 天时完成它。
第四门课现在不能修，因为你将会在第 3300 天完成它，这已经超出了关闭日期。

提示:

  1. 整数 1 <= d, t, n <= 10,000 。
  2. 你不能同时修两门课程。

思路：典型的贪心算法，课程开始时间无限制。

假设有两个课程，[t1,d1],[t2,d2]（d1<d2）,现在的时间是t

那么要修这两个课程,

如果先修[t1,d1]。要满足的条件是x+t1<d1 , x+t1+t2<d2

如果先修[t2,d2]。要满足的条件是x+t1+t2<d1,x+t1+t2<d2

显然先修[t1,d1]更好，也就是先修结束时间早的课程。

按结束时间排序，然后遍历修课程

那么当修了前面时间早的课程，时间超过了当前想要修的课程的时候，必须要丢一个课程，那么可以从前面修的课程里面挑一个用时最长的课程跟现在的课程比较，修二者时间短的课程，方便后面修其他课程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int scheduleCourse(vector<vector<int>>& courses) {
        sort(courses.begin(),courses.end(),[&](vector<int>&a,vector<int>&b){
            return a[1]<b[1];
        });			//按结束时间排序
        priority_queue<int ,vector<int>,less<int>> pque;//大顶堆存放修的课程的用时
        int time=0;				//当前时间
        for(auto& x:courses){
            time+=x[0];			//选择修现在的课程
            pque.push(x[0]);	//将现在的课程时间放入堆
            if(time>x[1]){		//如果现在的课程修不了
                time-=pque.top();	//删除修的课程最大的
                pque.pop();
            }
        }
        return pque.size(); 	//堆的元素数量就是答案
    }
};

链表

easy

相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

img

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

思路1：预处理两个链表的长度，再从长链表的尾开始倒数短链表的长度，开始同时遍历。

思路2：每个链表从头开始遍历，遍历完了，继续从另一个头开始遍历，直到遇到第一个相同的节点。

相同的节点为空就是两个链表不相交。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode *ha=headA, *hb=headB;
        while(ha!=hb){
            ha=(ha==NULL)?headB:ha->next;
            hb=(hb==NULL)?headA:hb->next;
        }
        return ha;
    }
};

medium

删除排序链表中的重复元素 II

存在一个按升序排列的链表，给你这个链表的头节点 head ，请你删除链表中所有存在数字重复情况的节点，只保留原始链表中 没有重复出现 的数字。

返回同样按升序排列的结果链表。

1
2
输入：head = [1,2,3,3,4,4,5]
输出：[1,2,5]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        ListNode* tmphead= new ListNode(0,head);	//哨兵
        ListNode* pre=tmphead;	//前一个
        ListNode* cur=head;		//当前节点
        ListNode* next=nullptr;	//下一个节点
        while(cur){			//处理当前节点
            int count=0;	//重复个数
            next=cur->next;
            while(next&&next->val==cur->val){//计算重复个数
                count++;
                next=next->next;
            }
            if(count!=0){		//有重复个数
                pre->next=next;//连接下一个cur
                cur=next;//cur等于下一个要判断的节点
            }else{		//没有重复个数
                pre=cur;		//前进一格
                cur=cur->next;	//前进一格
            }
        }
        return tmphead->next;
    }
};

hard

合并K个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

1
2
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]

思路1：将所有的链头放入小顶堆，每次选堆里最小的链头，连接到答案链表的尾部，选的链头如果还有后序节点，继续放入后序节点的链头。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        auto cmp=[](ListNode* & l1,ListNode* & l2){return l1->val>l2->val;};
        //自定义比较函数的小顶堆
        priority_queue<ListNode*, vector<ListNode*>,decltype(cmp)> pque(cmp);
        for(auto& list:lists){//加入所有链表头
            if(list){
                pque.push(list);
            }
        }
        ListNode* head=new ListNode();//哨兵链表头
        ListNode* cur=head;
        while(!pque.empty()){
            cur->next=pque.top();//往队尾加
            pque.pop();
            cur=cur->next;
            if(cur->next){		//还有后续节点
                pque.push(cur->next);
            }
        }
        return head->next;
    }
}

思路2：分治链表，将所有链表两两合并，合并的链表再次两两合并，如此类推。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return mergeLists(lists,0,lists.size()-1);
    }
    ListNode* mergeLists(vector<ListNode*>& lists,int left,int right){//分治k个链表
        if(left==right)
            return lists[left];
        if(left>right) 				//注意这里返回空
            return nullptr;
        int mid=left+(right-left)/2;
        return mergeTwoLists(mergeLists(lists,left,mid),mergeLists(lists,mid+1,right));
    }
    ListNode* mergeTwoLists(ListNode* l1,ListNode* l2){			//递归合并两个链表
        if(l1&&l2){
            if(l1->val>l2->val){
                l2->next=mergeTwoLists(l1,l2->next);
                return l2;
            }else{
                l1->next=mergeTwoLists(l1->next,l2);
                return l1;
            }
        }else{
            return (l1==nullptr)?l2:l1;
        }
    }
};

K 个一组翻转链表

给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。

k 是一个正整数，它的 1值小于或等于链表的长度。

如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

进阶：

  • 你可以设计一个只使用常数额外空间的算法来解决此问题吗？
  • 你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

思路：k组头插法，每次区间翻转（start，tail]。

注意翻转后和后一段未反转段的拼接。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    ListNode* reverseGroup(ListNode* start,ListNode* tail){ //反转区间(start,tail]
        ListNode* Pend=start->next; //本段翻转后的最后一个
        ListNode* cur=start->next,*tmp=nullptr;//cur当前翻转节点，tmp未翻转前cur后一个节点
        while(cur){
            tmp=cur->next;          //保存未翻转前cur后一个节点
            cur->next=start->next;  //cur插到头节点后
            start->next=cur;
            if(cur==tail)          	//cur是最后一个翻转的节点
                break;
            cur=tmp;                //继续翻转原序列的cur后一个节点
        }
        Pend->next=tmp;             //区间最后一个节点连接上翻转区间后的节点（tail->next）
        return Pend;                //返回翻转后区间的最后的节点
    }
    ListNode* reverseKGroup(ListNode* head, int k) {
        if(k == 1)return head;
        ListNode* newhead=new ListNode(0,head);  //虚拟头结点
        ListNode* fast=newhead,*slow=newhead;
        while(fast){
            for(int i=0;i<k;++i){           //走k步才到最后的节点
                fast = fast -> next;
                if(fast==nullptr)           //提前结束
                    return newhead->next;
            }
            slow=reverseGroup(slow,fast);   //翻转后返回最后的节点
            fast=slow;                      //fast和slow都在最后的节点
        }
        return newhead->next;
    }
};

数学

easy

圆圈中最后剩下的数字

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

思路：约瑟夫环，可以递归或动态规划解决。

要删除的nums序号
0 1 2 3 4 2
3 4 0 1 2
1 3 4 2
1 3 0
3 0

整个表格反过来(k=3)

要找的nums序号
3 0 最后一个,也就是要留下来的数
1 3 1 =(0+k)%2 序号0后面补上走了k步，找到了3
1 3 4 1 =(1+k)%3 序号1后补上k步，找到了3
3 4 0 1 0 =(1+k)%4 序号1后补上k步，找到了3
0 1 2 3 4 3 =(0+k)%5 序号0后补上k步，找到了3

由于序号等于nums[序号]，所以最后返回的是最后一步要删的数在n长度数组的位置也就是nums[序号]

递归版

1
2
3
4
5
6
7
class Solution {
public:
    int lastRemaining(int n, int m) {
        if(n==1) return 0;
        else return (lastRemaining(n-1,m)+m)%n;
    }
};

动态规划版

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int lastRemaining(int n, int m) {
        int index=0;
        for(int i=2;i<=n;++i){
            index=(index+m)%i;
        }
        return index;
    }
};

排序

1996. 游戏中弱角色的数量

你正在参加一个多角色游戏，每个角色都有两个主要属性：攻击 和 防御 。给你一个二维整数数组 properties ，其中 properties[i] = [attacki, defensei] 表示游戏中第 i 个角色的属性。

如果存在一个其他角色的攻击和防御等级 都严格高于 该角色的攻击和防御等级，则认为该角色为 弱角色 。更正式地，如果认为角色 i 弱于 存在的另一个角色 j ，那么 attackj > attacki 且 defensej > defensei 。

返回 弱角色 的数量。

思路：pre[]代表之前遍历的矩阵，v[0]代表当前遍历到的矩阵。

保证pre[0]>=v[0]的前提下，使得pre[1]<v[1]。

记录历史最大的pre[1]与v[1]比较，如果严格小于，则有pre[0]<v[0]&&pre[1]<v[1]

image-20220128023850453

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int numberOfWeakCharacters(vector<vector<int>>& properties) {
        sort(properties.begin(),properties.end(),[&](vector<int>& v1,vector<int>& v2){
            return (v1[0]==v2[0])?(v1[1]<v2[1]):(v1[0]>v2[0]);
        });
        int n=properties.size(),ans=0;
        int maxdef=0;
        for(auto& v:properties){
            (v[1]<maxdef)?ans++:maxdef=v[1];
        }
        return ans;
    }
};

其他

medium

把数组排成最小的数

输入一个非负整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。

示例 1:

1
2
输入: [10,2]
输出: "102"

思路：自定义排序，将两个数拼接在一起，判断哪个数在前面更小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    string minNumber(vector<int>& nums) {
        vector<string> strs;
        for(const int& num:nums)
            strs.emplace_back(to_string(num));
        sort(strs.begin(),strs.end(),[](string& a,string& b){
            return a+b<b+a;
        });
        string ans="";
        for(const string& str:strs)
            ans+=str;
        return ans;
    }
};

构建乘积数组

给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。

示例:

1
2
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]

思路：注意不能使用除法，而且就算使用除法也需要判断 A[i]是不是等于0，

可以分两次遍历完成，第一遍从前往后遍历把 A[0]×A[1]×…×A[i-1]存入 B[i]

第二遍从后往前遍历把 A[n-1]×A[n-2]×…×A[i+1]乘上 B[i]放入 B[i]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<int> constructArr(vector<int>& a) {
        vector<int> ans(a.size());
        for(int i=0,base=1;i<a.size();++i){
            ans[i]=base;
            base*=a[i];
        }
        for(int i=a.size()-1,base=1;i>=0;--i){
            ans[i]=ans[i]*base;
            base*=a[i];
        }
        return ans;
    }
};

数值的整数次方

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，x^n）。不得使用库函数，同时不需要考虑大数问题。

示例 1：

1
2
输入：x = 2.00000, n = 10
输出：1024.00000

示例 3：

1
2
3
输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25
1
2
3
4
范围：
	-100.0 < x < 100.0
	-2^31 <= n <= 2^31-1
	-10^4 <= x^n <= 10^4

思路：考察快速幂x^n

时间复杂度O($log_2(n)$)

空间复杂度O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    double myPow(double x, int n) {
        long tmpn=n;//由于-2^31取相反数时会超过int范围，先将n存放在long类型
        if(n<0){
            x=1/x;
            tmpn=-tmpn;
        }
        double ans=1;
        while(tmpn){
            if(tmpn&1)
                ans*=x;
            x*=x;
            tmpn>>=1;
        }
        return ans;
    }
};

递归版

1
2
3
4
5
6
7
double recurPow(double x,int n){
    if(n==0) return 1;
    //处理负数n
    if(n==-1) return 1/x;
    if(n&1) return recurPow(x*x,n>>1)*x;
    else return recurPow(x*x,n>>1);
}

剪绳子 II

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m - 1] 。请问 k[0]*k[1]*...*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

思路：数学求导得到每一段都为3时，相乘是最优解。

分为4种情况

2<=n<=3时返回n-1，因为 m>1

当对3求余得到0直接返回3的段数次方

当对3求余得到1返回3的（段数-1）次方乘以4（最后一段长度为3的段取出来，分成2，2）

当对3求余得到2返回3的段数次方*2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int modnum=1000000007;
    //快速幂求base^exp%modnum
    long FastPowAndMod(long base,int exp){
        long ans=1;
        while(exp){
            if(exp&1){
                ans*=base;
                ans%=modnum;
            }
            base*=base;
            base%=modnum;
            exp>>=1;
        }
        return ans;
    }
    int cuttingRope(int n) {
        if(n<=3)return n-1;
        int segnum=n/3;
        int remain=n%3;
        switch(remain){
            case 0:return FastPowAndMod(3,segnum);
            case 1:return FastPowAndMod(3,segnum-1)*4%modnum;
            default:return FastPowAndMod(3,segnum)*2%modnum;
        }
    }
};

数组中数字出现的次数 II

在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。

示例 1：

1
2
输入：nums = [3,4,3,3]
输出：4

思路：统计二进制每一位的1的数量，余3后剩余的数只会是1或0，拼接这些二进制就可以得到答案。

时间复杂度O(n)

空间复杂度O(1)

3: 0 1 1
4: 1 0 0
3: 0 1 1
3: 0 1 1
sum 1 3 3
sum%3 1 0 0 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans=0;
        for(int i = 0;i < 31; ++i){
            int count=0;			//统计第i位1的数量
            for(int num:nums){		//遍历数组
                count+=(num>>i&1);	//添加num的第i位1的数量
            }
            ans+=(count%3)<<i;		//拼接到ans,注意这里count%3只会为0或1
        }
        return ans;
    }
};

有效的数独

请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

数独部分空格内已填入了数字，空白格用 '.' 表示。

思路：每一个行，一个列，一个9宫格都用一个bitset<9>记录之前是否有这个数。

对于 board[ i ] [ j ] 来说他在第i行第j列第(int)(i/3)*3+j/3个宫格。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        bitset<9> rowset[9],colset[9],boxset[9];
        for(int i=0;i<9;++i){
            for(int j=0;j<9;++j){
                if(board[i][j]!='.'){
                    int val=board[i][j]-'1';
                    int boxindex=i/3*3+j/3;
					if(!rowset[j].test(val)&&!colset[i].test(val)&&!boxset[boxindex].test(val)){
                        rowset[j].set(val);
                        colset[i].set(val);
                        boxset[boxindex].set(val);
                    }else return false;
                }
            }
        }
        return true;
    }
};

hard

有效数字

有效数字（按顺序）可以分成以下几个部分：

  1. 一个 小数 或者 整数
  2. （可选）一个 'e' 或 'E' ，后面跟着一个 整数

小数（按顺序）可以分成以下几个部分：

  1. （可选）一个符号字符（'+' 或 '-'）
  2. 下述格式之一：
    1. 至少一位数字，后面跟着一个点 '.'
    2. 至少一位数字，后面跟着一个点 '.' ，后面再跟着至少一位数字
    3. 一个点 '.' ，后面跟着至少一位数字

整数（按顺序）可以分成以下几个部分：

  1. （可选）一个符号字符（'+' 或 '-'）
  2. 至少一位数字

部分有效数字列举如下：

  • ["2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e+7", "+6e-1", "53.5e93", "-123.456e789"]

部分无效数字列举如下：

  • ["abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"]

给你一个字符串 s ，如果 s 是一个 有效数字 ，请返回 true 。

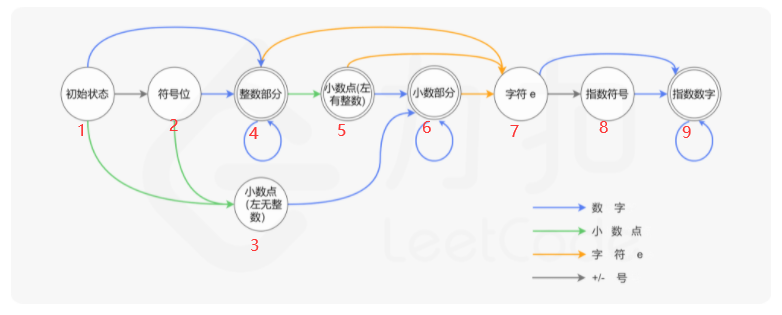
思路：建立有限状态转换机，借用leetcode的图。

状态图.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class Solution {
public:
    bool isNumber(string s) {
        int status=1;
        int i=0;
        while(i<s.size()){
            switch(status){
                case 1:{
                    if(isdigit(s[i]))
                        status=4;
                    else if(s[i]=='.')
                        status=3;
                    else if(s[i]=='+'||s[i]=='-')
                        status=2;
                    else return false;
                    break;
                }
                case 2:{
                    if(isdigit(s[i]))
                        status=4;
                    else if(s[i]=='.')
                        status=3;
                    else return false;
                    break;
                }
                case 3:{
                    if(isdigit(s[i]))
                        status=6;
                    else return false;
                    break;
                }
                case 4:{
                    if(s[i]=='.')
                        status=5;
                    else if(isdigit(s[i])){}
                    else if(s[i]=='e'||s[i]=='E')
                        status=7;
                    else return false;
                    break;
                }
                case 5:{
                    if(isdigit(s[i]))
                        status=6;
                    else if(s[i]=='e'||s[i]=='E')
                        status=7;
                    else return false; 
                    break;
                }
                case 6:{
                    if(s[i]=='e'||s[i]=='E')
                        status=7;
                    else if(isdigit(s[i])){}
                    else return false;
                    break;
                }
                case 7:{
                    if(isdigit(s[i]))
                        status=9;
                    else if(s[i]=='+'||s[i]=='-')
                        status=8;
                    else return false;
                    break;
                }case 8:{
                    if(isdigit(s[i]))
                        status=9;
                    else return false;
                    break;
                }case 9:{
                    if(!isdigit(s[i]))
                        return false;
                    break;
                }
                default:{
                    return false;
                }
            }
            ++i;
        }
        return status==4||status==5||status==6||status==9;
    }
};
本文链接：
https://ioaol.github.io/leetcode%E7%AC%94%E8%AE%B0.html